Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

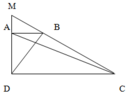
a. S A B C = 1 3 S A D C (Vì cùng chung chiều cao của hình thang ABCD; đáy AB = 1 3 DC)
b. S A B M = S A C M (Vì cùng chung đáy MA, chiều cao AB = 1 3 DC )
c. Theo phần a, ta có: S A B C = S A D C
Mà S A B C D = S A B C + S A D C
Nên S A B C = 1 1 + 3 S A B C D = 1 4 S A B C D
Do đó S A B C D = 64 × 1 4 = 16 ( c m 2 )
Theo phần b, ta có: S A B M = 1 3 S A C M
Mà S A C M = S M A B + S A B C
Nên S M A B = 1 3 - 1 S A B C = 1 2 S A B C
Do đó S M A B = 16 × 1 4 = 8 ( c m 2 )

Xin loi bai nay minh ko ve duoc hinh.Thong cam cho minh nhe !!!
a)S_ABC = 1/3 S_ADC (Đáy AB = 1/3 đáy CD; Chiều cao hạ xuống đáy từ C bằng chiều cao hạ từ A)
b)S_ABM = 1/3 S_CAM (Đáy AM chung; chiều cao hạ từ B bằng 1/3 chiều cao hạ từ B xuống đáy AM)
c)
S_ABC = 1/3 S_ACD (câu trên) => S_ABC = 1/4 S_ABCD = 64 : 4 = 16 cm2
Mà: S_ABM = 1/3 S_ACM (câu trên) => S_ABM = 1/2 S_ABC = 16 : 2 = 8 cm2

Bài giải
a) Do đề bài không cập nhật độ dài của hình thang ABCD nên ta gọi chiều cao là AD ( với AD = BC ), độ dài cạnh DC là 13 ×3=1cm. Vậy, diện tích hình tam giác ABC là :
13 ×AD2 =16 AD( cm2 )
Diện tích hình tam giác ADC là :
\(\frac{1\times AD}{2}=\frac{1}{2}AD\left(cm^2\right)\)
Vì : \(\frac{1}{6}AD< \frac{1}{2}AD\)
nên diện tích hình tam giác ADC lớn hơn diện tích hình tam giác ABC.
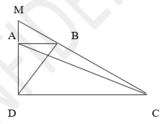

a/ Xét tg ABD và tg CBD có đường cao từ D->AB = đường cao từ B->CD nên
\(\frac{S_{ABD}}{S_{CBD}}=\frac{AB}{CD}=\frac{2}{5}\)
b/
Gọi O là giao của AC và BD, nối M với O cắt AB tại I
Ta có \(\frac{S_{ABD}}{S_{CBD}}=\frac{2}{5}\) Hai tg này có chung cạnh BD nên
\(\frac{S_{ABD}}{S_{CBD}}=\) đường cao từ A->BD / đường cao từ C->BD \(=\frac{2}{5}\)
Xét tg ABO và tg BCO có chung cạnh BO nên
\(\frac{S_{ABO}}{S_{BCO}}=\)đường cao từ A->BD / đường cao từ C->BD \(=\frac{2}{5}\) Hai tg này có chung đường cao từ B->AC nên
\(\frac{S_{ABO}}{S_{BCO}}=\frac{AO}{CO}=\frac{2}{5}\)
Xét tg AMO và tg CMO có chung đường cao từ M->AC nên
\(\frac{S_{AMO}}{S_{CMO}}=\frac{AO}{CO}=\frac{2}{5}\) Hai tg này có chung cạnh MO nên
\(\frac{S_{AMO}}{S_{CMO}}=\) đường cao từ A->MO / đường cao từ C->MO \(=\frac{2}{5}\)
Xét tg AMI và tg CMI có chung cạnh MI nên
\(\frac{S_{AMI}}{S_{CMI}}=\)đường cao từ A->MO / đường cao từ C->MO \(=\frac{2}{5}\Rightarrow S_{AMI}=\frac{2xS_{CMI}}{5}\)
Chứng minh tương tự ta cũng có
\(\frac{S_{BMI}}{S_{DMI}}=\frac{2}{5}\Rightarrow S_{BMI}=\frac{2xS_{DMI}}{5}\)
\(\Rightarrow S_{AMI}+S_{BMI}=\frac{2}{5}x\left(S_{CMI}+S_{DMI}\right)=\frac{2}{5}x\left(S_{BMI}+S_{BIC}+S_{AMI}+S_{AID}\right)\)
\(\Rightarrow\frac{3}{5}x\left(S_{AMI}+S_{BMI}\right)=\frac{2}{5}x\left(S_{BIC}+S_{AID}\right)\)
\(\Rightarrow\frac{3}{5}xS_{AMB}=\frac{2}{5}x\left(S_{BIC}+S_{AID}\right)\) (*)
Xét tg AID và tg AIC có chung cạnh AI và đường cao từ D->AB = đường cao từ C->AB nên \(S_{AID}=S_{AIC}\) Thay vào (*)
\(\Rightarrow\frac{3}{5}xS_{AMB}=\frac{2}{5}x\left(S_{BIC}+S_{AIC}\right)=\frac{2}{5}xS_{ABC}\Rightarrow\frac{S_{AMB}}{S_{ABC}}=\frac{2}{3}\)
Xét tg AMB và tg ABC có chung đường cao từ A->MC nên
\(\frac{S_{AMB}}{S_{ABC}}=\frac{MB}{BC}=\frac{2}{3}\)