Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: BD // MN
=> Khoảng cách từ BD đến MN = khoảng cách từ MN đến BD
Và gọi khoảng cách đó là h
\(\Rightarrow\hept{\begin{cases}S_{\Delta BMN}=\frac{1}{2}h\cdot MN\\S_{\Delta DMN}=\frac{1}{2}h\cdot MN\end{cases}}\Rightarrow S_{\Delta BMN}=S_{\Delta DMN}\)
b) \(\frac{S_{\Delta DMA}}{S_{\Delta DAC}}=\frac{MA}{AC}=\frac{1}{2}\Rightarrow S_{\Delta DMA}=\frac{1}{2}S_{\Delta DAC}\)
\(\frac{S_{\Delta ABM}}{S_{\Delta ABC}}=\frac{MA}{AC}=\frac{1}{2}\Rightarrow S_{\Delta ABM}=\frac{1}{2}S_{\Delta ABC}\)
\(\Rightarrow S_{\Delta DMA}+S_{\Delta ABM}=\frac{1}{2}\cdot\left(S_{\Delta DAC}+S_{\Delta ABC}\right)\)
\(\Rightarrow S_{ABMD}=\frac{1}{2}\cdot16=8\left(cm^2\right)\)

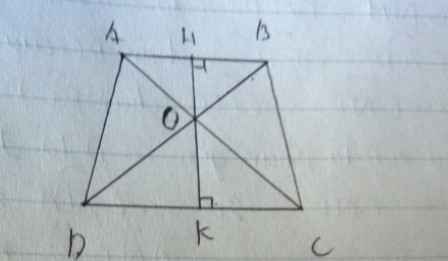
\(ABssCD\Rightarrow\dfrac{AB}{CD}=\dfrac{OB}{OD}=\dfrac{OA}{OC}=\dfrac{2}{3}\)
a)\(S_{AOD}=\dfrac{1}{2}OA.OD.sinAOB\)
\(S_{BOC}=\dfrac{1}{2}OB.OC.sinBOC\)
\(\Rightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{OA.OD}{OB.OC}\) vì \(\widehat{AOD}=\widehat{BOC}\Rightarrow sinAOD=sinBOC\)
\(\Leftrightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{2}{3}.\dfrac{3}{2}=1\)
b) vì \(ABssCD\Rightarrow\dfrac{OH}{OK}=\dfrac{2}{3}\Rightarrow\dfrac{OH}{HK}=\dfrac{2}{5}\)
\(S_{AOB}=\dfrac{1}{2}.OH.AB\\ S_{ABCD}=\dfrac{1}{2}\left(AB+CD\right).HK=\dfrac{1}{2}\left(AB+\dfrac{3}{2}AB\right).HK=\dfrac{1}{2}.\dfrac{5}{2}AB.HK\)
\(\Rightarrow\dfrac{S_{AOB}}{S_{ABCD}}=\dfrac{\dfrac{1}{2}OH.AB}{\dfrac{1}{2}HK.\dfrac{5}{2}AB}=\dfrac{2}{5}.\dfrac{1}{\dfrac{5}{2}}=\dfrac{4}{25}\)
\(\Rightarrow S_{ABCD}=\dfrac{4}{\dfrac{4}{25}}=25\)
MN//BD
=>d(N;BD)=d(M;BD)
\(S_{DBN}=\dfrac{1}{2}\cdot d\left(N;BD\right)\cdot BD;S_{DBM}=\dfrac{1}{2}\cdot d\left(M;BD\right)\cdot BD\)
=>\(S_{DBN}=S_{DBM}\)
mà \(S_{ABND}=S_{ADB}+S_{BDN}\)
nên \(S_{ABND}=S_{ADB}+S_{DBM}\)
\(=S_{AOD}+S_{ABO}+S_{OMD}+S_{OBM}\)
\(=S_{ADM}+S_{ABM}\)
\(=\dfrac{1}{2}\cdot\left(S_{ADC}+S_{ABC}\right)=\dfrac{1}{2}\cdot S_{ABCD}=8\left(cm^2\right)\)