
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



bạn tham khảo tại đây nhé, mk bận ko thể giải cho bn dc, thông cảm nha, h mk phải ik ăn đám cứ r, chúc bn hc tốt nhé
http://pitago.vn/question/a-dung-hinh-thang-abcd-ab-cd-biet-day-ab-2-cm-hai-10453.html
trên CD lấy điểm H sao cho DH=AB
Tứ giác ABHD có DH=AB và DH//AB
=>ABHD là HBH
=>AD=BH
DH+HC=CD
2+HC=5
=>HC=3
áp dụng BĐT tam giác trong tam giác BHC ta có
BH+BC>HC
hay AD+BC>3

Đề sửa lại: Hình thang ABCD ( AB//CD ) có AB=2cm CD=5cm. Chứng minh rằng AD + BC>3cm
Giải:
Tg ADC có DC - AD < AC (bất đằng thức tam giác)(1)
tg ABC có AC < AB + BC (bất đằng thức tam giác)(2)
Từ (1) và (2) => DC - AD < AB + BC => DC - AB < AB + BC
mà AB=2cm CD=5cm => 5 - 2 < AB + BC hay AB + BC > 3 (đpcm)
Chúc bạn thành công!
Giải: (sửa giúp)
...v.v...
Từ (1) và (2) => DC - AD < AB + BC => DC - AB < AD + BC

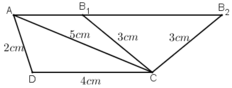
* Dựng hình:
- Dựng tam giác ADC có AD = 2cm, DC = 4cm, CA = 5cm.
- Dựng tia Ax song song với CD.
- Đường tròn (C; 3cm) cắt Ax tại B1 và B2.
Hình thang ABCD với B ≡ B1 hoặc B ≡ B2 là hình thang cần dựng.
* Chứng minh
+ Tứ giác ABCD có AD = 2cm, DC = 4cm, CA = 5cm.
+ Ax // CD ⇒ AB // CD ⇒ ABCD là hình thang.
+ B ∈ (C; 3cm) ⇒ BC = 3cm.

Chung minh ABD đồng dạng với BDC
=> \(\widehat{ABD}\)=\(\widehat{BDC}\)
hai góc này ở vị trí sole trong
=> AB//CD

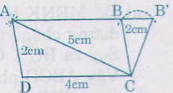
Dựng đoạn thẳng CD = 4cm.
- Dựng hai đường tròn (C, 5cm) và (D, 2cm) cắt nhau tại A.
- Dựng đường tròn (C, 2cm) và đường tròn (A, 4cm) cắt nhau tại B.
Đường thẳng AB kéo dài cắt đường tròn (C, 2cm) tại điểm B' (ngoài điểm B đã kể ở trên)
Các tứ giác ABCD và AB'CD là những hình thang thỏa mãn đề bài.
Chứng minh: Vì B thuộc đường tròn (A, 4cm) nên AB = 4cm.
ΔABC = ΔDCA (AB = CD = 4cm, AD = BC = 2cm, AC chung) do đó góc BAC = góc DCA là cặp so le trong ta có: AB // CD.
Tứ giác ABCD có AB // CD, AD = 2cm, CD = 4cm, BC = 2cm là hình thang thỏa mãn yêu cầu, AB'CD cũng là hình thang thỏa mãn yêu cầu vì AB' // CD, AD = 2cm, CD = 4cm, CB' = 2cm.
tự vẽ hình nha bạn
Vẽ BE \(//\)AC (\(E\in AC\))
Ta có AB \(//\)CE (AB\(//\)CD)
nên ABEC là hình thang có 2 đáy là AB và CE
mà BE\(//\)AC
nên AC = BE; AB = CE (=2cm)
Ta có CD = CE + DE
nên 5 = 2 + DE
do đó DE = 5 - 2 = 3(cm)
Xét ΔBED
Ta có BE + BC > DE (bất đẳng thức tam giác)
mà BE = AC; DE = 3 cm (cmt)
nên AC + BC > 3cm