Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi P và Q lần lượt là giao điểm của AE, AF với CD.
Chứng minh tương tự 2B.
b) Ta có:
M N = 1 2 ( A B + C D ) = 1 2 ( a + c )
Lại có:
c = CD = CQ + QD = BC + QD = b + QD (do tam giác BCQ cân) Þ QD = c - b.
Trong hình thang ABQD có M là trung điểm của AD và MF//DQ nên chứng minh được F là trung điểm của BQ, từ đó chứng minh MF là đường trung bình của hình thang ABQD.
Vì MF là đường trung bình của hình thang ABQD.
Þ M F = 1 2 ( A B + D Q ) = 1 2 ( a + c − b )
Mặt khác, FN là đường trung bình của tam giác BCQ, tức là F N = 1 2 C Q = 1 2 b .
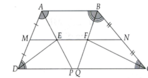
Gọi I là giao điểm của AC với EF.
Xét ΔADC có EI // DC, theo định lý Ta-lét ta có: A E A D = A I A C (1)
Xét ΔABC có IF // AB, theo định lý Ta-lét ta có: A I A C = B F B C (2)
Từ (1) và (2) suy ra A E A D = B F B C
⇒ E D A D + B F B C = E D A D + A E A D = E D + A E A D = A D A D = 1
Do đó E D A D + B F B C = 1 hay A đúng
Đáp án: A