Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ABD và BDE có Ab=BE , và có chung cạnh BD
=> ABD =BED =9cm2
DC=1/3 BC => DC=1/2 BD
ABD và ACD có DC=1/2 BD và chung đường cao hạ từ đỉnh C
=> ADC = 1/2 ABD = 1/2x9=4,5cm2
=> S. ABC = 9+4,5=13,5cm2
Xét ΔACB có
AD là trung tuyến
AE=2/3*AD
=>E là trọng tâm
=>\(S_{ABE}=\dfrac{1}{3}\cdot S_{ACB}\)
=>\(S_{ABC}=40.5\left(cm^2\right)\)
Vì BD =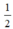 
DC nên diện tích tam giác ABD = 
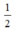diện tích tam giác ADC (do hai tam giác có cùng chiều cao)
Diện tích tam giác ADC là:
24 x 2 = 48 (cm2)
Diện tích tam giác ABC là:
24 + 48 = 72 (cm2)
Đáp số: 72 cm2.
Xét hai tam giác ABD và BED :
- Chung chiều cao hạ từ đỉnh B xuống cạnh AD
- AD = 3/2 ED
=> SABD = SEBD x 3/2 = 4,5 x 3/2 = 6,75 ( cm2)
Xét hai tam giác ABC và ABD :
- Chung chiều cao hạ từ đỉnh A xuống cạnh BC
- BC = 3 lần BD
=> SABC = 3 x SABD = 6,75 x 3 = 20,25 ( cm2)
Vậy diện tích tam giác ABC là : 20,25 cm2
Vì BD=1/2DC nên BD=1/3 AC . Suy rA ABD=1/3 ABC =>ABC=72(cm2)
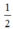
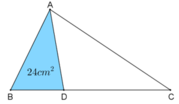
a: S ABE=S EBD=1/2*S ABD
DC=1/2DB
nên S ADC=1/2*S ABD
=>S ABE=S EBD=S ADC
b: S ABC=3/2*24=36cm2