Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì hình tam giác ABC có 1 góc vuông nên hình tam giác ABC là tam giác vuông. Diện tích hình tam giác ABC là:
30 x 30 : 2 = 450 (cm2)
Diện tích hình tam giác AMC là:
450 : 2 = 225 (cm2)
Vì AB và AC = nhau nên cạnh AB có độ dài là: 30 cm
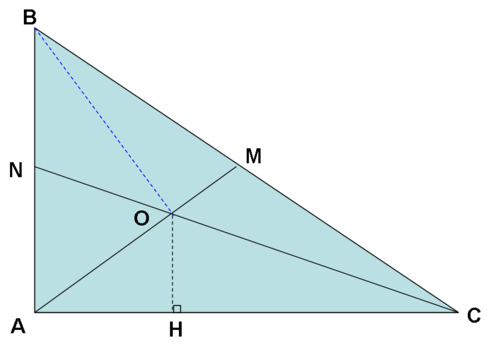
Nhìn vào hình tam thấy hình tam giác OMC = 1/3 hình tam giác AOC nên đồng nghĩa với việc hình tam giác AOC chiếm 1 - 1/3 = 2/3 Diện tích hình tam giác AMC. Diện tích hình tam giác AOC là:
225 : 3 x 2 = 150 cm2
Chiều cao hạ từ đỉnh O của hình AOC là:
150 : 30 = 5 cm
ĐS: 5 cm
tk nha

Xét tam giác OBM và ONC chung đỉnh O, M là điểm chính giữa BC => SOBM = S_ONC (1)
Xét tám giác ABM và AMC chung đỉnh A, M là điểm chính giữa BC => SABM = S_ANC (2)
Từ (1) và (2) ta có S_ABO = S_AOC
Mặt khác S_NBO = S_ANO vì chung điểm O , BN=NA
Vậy S_NNO = 1/2 S_AOC => S_OCA = 2/3 S_ANC
=> ON = 2/3 NA (tam giác ANC và OCA chung đáy AC)
Vậy đường cao kẻ từ O của tam giác AOC là : 30 : 2 x 2/3 = 10 (cm)
Đáp số:10 cm
Ai tích mình mình tích lại cho

Diện tích tam giác \(ABC\)là:
\(60\times40\div2=1200\left(cm^2\right)\)
Có: \(S_{ABC}=S_{ANM}+S_{BND}+S_{CDM}+S_{DMN}\)
\(\Leftrightarrow S_{DMN}=S_{ABC}-S_{ANM}-S_{BND}-S_{CDM}\)
Để tích diện tích tam giác \(DMN\)ta sẽ tính diện tích các tam giác \(ANM,BND,CDM\).
\(S_{AMB}=\frac{1}{3}\times S_{ABC}\)(chung đường cao hạ từ \(B\), \(AM=\frac{1}{3}\times AC\))
\(S_{ANM}=\frac{1}{2}\times S_{AMB}\)(chung đường cao hạ từ \(M\), \(AN=\frac{1}{2}\times AB\))
suy ra \(S_{ANM}=\frac{1}{2}\times\frac{1}{3}\times S_{ABC}=\frac{1}{6}\times S_{ABC}\).
Một cách tương tự, ta cũng suy ra được \(S_{BND}=\frac{1}{2}\times\frac{1}{2}\times S_{ABC}=\frac{1}{4}\times S_{ABC}\)
\(S_{CDM}=\frac{1}{2}\times\frac{1}{3}\times S_{ABC}=\frac{1}{6}\times S_{ABC}\)
\(S_{DMN}=S_{ABC}-S_{ANM}-S_{BND}-S_{CDM}\)
\(=S_{ABC}-\frac{1}{6}\times S_{ABC}-\frac{1}{4}\times S_{ABC}-\frac{1}{6}\times S_{ABC}\)
\(=\frac{5}{12}\times S_{ABC}\)
\(=\frac{5}{12}\times1200=500\left(cm^2\right)\)