Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M, N lần lượt là trung điểm các cạnh A′B′,C′D′ ta có ((OA′B′), (OC′D′)) = (OM,ON).
Ta có
MN=a, 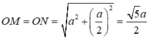
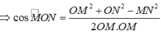
= 3 5
Chọn đáp án D.

Đáp án là A.
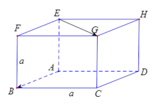
Ta có:
A B → . E G → = A B . E G . cos A B → ; E G → ^ = A B . A C . cos B A C ^ = a 2 2 . 2 2 = a 2 .

Phương pháp:
Phép đối xứng tâm O biến M thành M’=>O là trung điểm của MM’.
Cách giải:
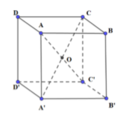
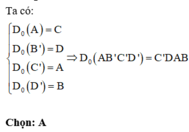

Câu 1:
\(\widehat{AOC}=180^0\cdot\dfrac{3}{4}=135^0\)
\(\widehat{BOC}=180^0-135^0=45^0\)
Câu 2:
a: Các cặp tia đối nhau là:
Ox' và Oy'
Ox và Oy
Câu b và c đề sai rồi bạn

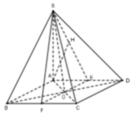
Gọi E, F lần lượt là trung điểm của AD, BC thì AB / / EF ⇒ AB / / (SEF)
Mà ![]()
![]()
Dựng A H ⊥ S E
Ta thấy: FE / / AB, A B ⊥ ( S A D ) ⇒ F E ⊥ ( S A D ) ⇒ F E ⊥ A H
Mà A H ⊥ S E nên A H ⊥ ( S E F ) ⇔ d ( A , ( S E F ) ) = A H
ABCD là hình vuông cạnh a nên B D = a 2
Dễ dàng chứng minh được ∆ S A B = ∆ S A D c . g . c ⇒ S B = S D
Tam giác SBD cân có S B D = 60 ° nên đều ⇒ S D = B D = a 2
Tam giác SAD vuông tại A có S A = S D 2 - A D 2 = 2 a 2 - a 2 = a
Tam giác SAE vuông tại A có


Do đó
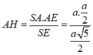
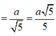
Chọn đáp án D.




Ta có. EG//AC (do ACGE là hình chữ nhật)
⇒ A B , E G = A B , A C = B A C = 45 o
Đáp án cần chọn là C