Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

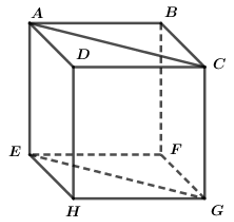
\(\overrightarrow{BD}.\overrightarrow{D'C}=\overrightarrow{BD}\left(\overrightarrow{D'D}+\overrightarrow{DC}\right)=\overrightarrow{BD}.\overrightarrow{D'D}+\overrightarrow{BD}.\overrightarrow{DC}\)
\(=\overrightarrow{BD}.\overrightarrow{DC}=-\overrightarrow{DB}.\overrightarrow{DC}=-a\sqrt{2}.a.cos45^0=-a^2\)

\(\overrightarrow{AB}.\overrightarrow{BD}=-\overrightarrow{BA}.\overrightarrow{BD}=-a.a.cos60^0=-\dfrac{a^2}{2}\)

Lời giải:$ABCD$ là hình vuông nên $AC=\sqrt{2}a$
Ta thấy: $SA^2+SC^2=a^2+a^2=2a^2=AC^2$
$\Rightarrow SAC$ là tam giác vuông tại $S$
$\Rightarrow \overrightarrow{SA}.\overrightarrow{SC}=0$

\(BD=a\sqrt{2}\)
\(\widehat{\left(\overrightarrow{BD};\overrightarrow{BS}\right)}=\widehat{SBD}=\dfrac{SB^2+BD^2-SD^2}{2SB.BD}=\dfrac{a^2+2a^2-a^2}{2a.a\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\widehat{\left(\overrightarrow{BD};\overrightarrow{BS}\right)}=45^0\)
thầy ơi bưa trước thầy em có giảng cái cách mà SB=SD thì suy ra SBD là nửa hình vuông nên góc SBD 45 độ v đúng ko thầy?
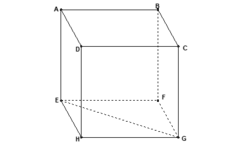
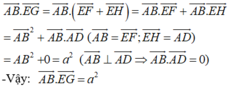



bài này ez mà :D ( Tự vẽ hình ) Vì EF // AB nên ta có thể viết như sau:
\(\overrightarrow{AB}.\overrightarrow{EG}=\overrightarrow{EF}.\overrightarrow{EG}=\overrightarrow{EF}\left(\overrightarrow{EF}+\overrightarrow{FG}\right)=EF^2+\overrightarrow{EF}.\overrightarrow{FG}=a^2\)
( Vì: \(\overrightarrow{EF}.\overrightarrow{FG}=\left|\overrightarrow{EF}\right|.\left|\overrightarrow{FG}\right|.\cos\left(\overrightarrow{EF},\overrightarrow{FG}\right)=0\)) ( \(\cos\left(\overrightarrow{EF},\overrightarrow{FG}\right)=90^0=0\))