

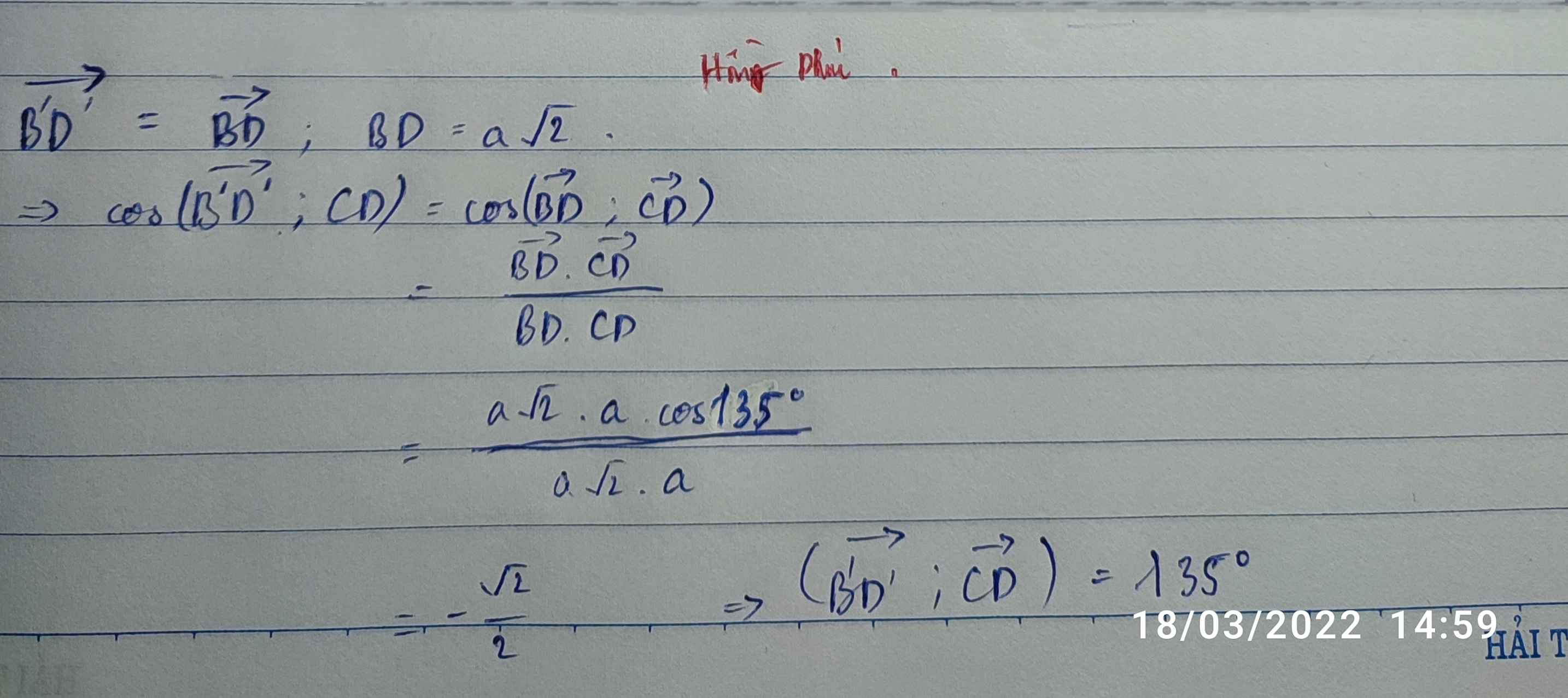
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


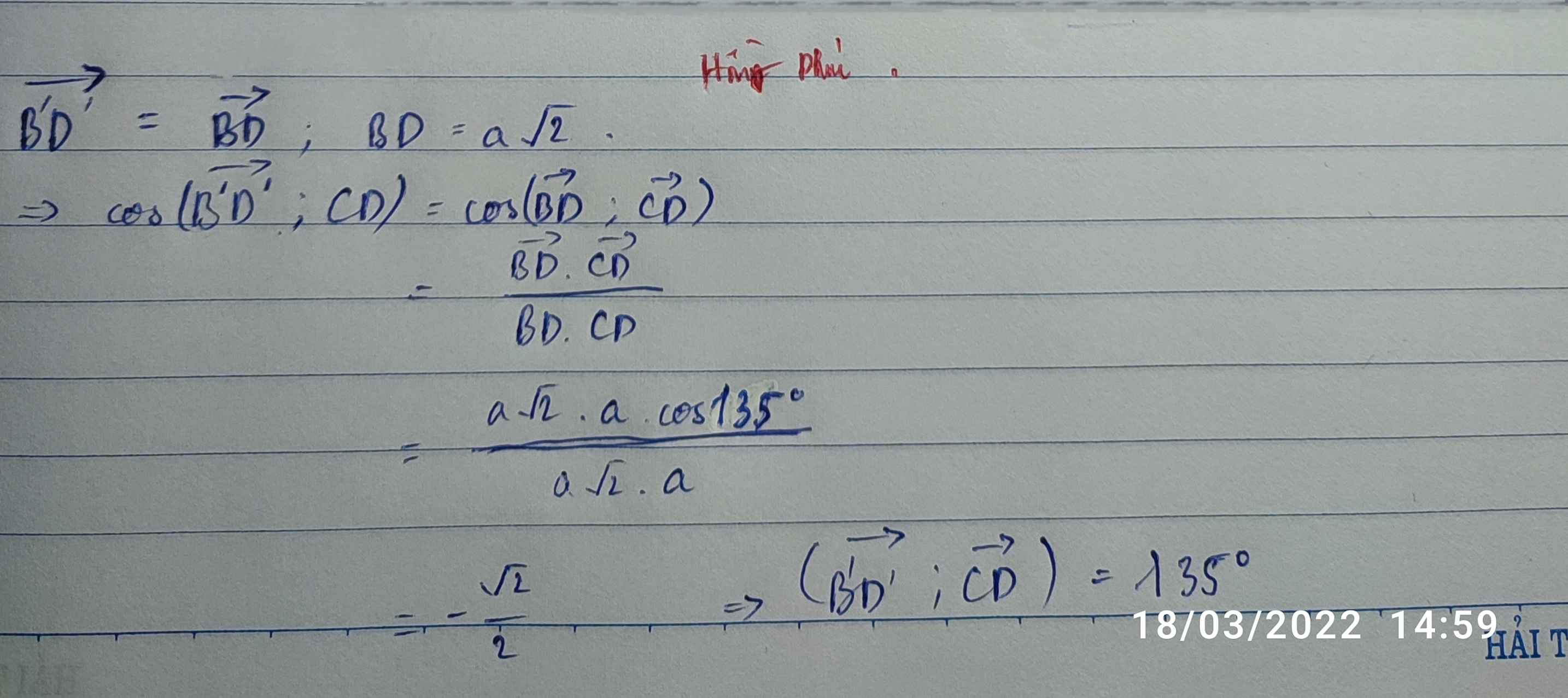
Cho hình lập phương ABCD.A'B'C'D'. Tính góc giữa hai đường thẳng AB' và CD'.
A. 600
B. 300
C. 900
D. 450

Ta có: \(CD'||A'B\)
Mà \(A'B\perp AB'\) (hai đường chéo hv)
\(\Rightarrow AB'\perp CD'\)

Do \(AC||A'C'\Rightarrow\widehat{\left(A'C';B'C\right)}=\widehat{\left(AC;B'C\right)}=\widehat{ACB'}\)
\(AC=AB'=B'C=AB\sqrt{2}\Rightarrow\Delta ACB'\) đều
\(\Rightarrow\widehat{ACB'}=60^0\)

Lời giải:
Coi \(ABCD\) là mặt đáy.
Trên tia đối của tia $BA$ lấy $T$ sao cho $BT=BA$. Khi đó:
\(\overrightarrow {AB}=\overrightarrow{BT}; \overrightarrow{CT}=\overrightarrow{DB}\)
Ta có:
\(\overrightarrow{OM}=\frac{1}{2}(\overrightarrow{a}-\overrightarrow{b})\)
\(\Leftrightarrow 2\overrightarrow{OM}=\overrightarrow{AB}-\overrightarrow{BC}=\overrightarrow{BT}-\overrightarrow {BC}\)
\(\Leftrightarrow 2\overrightarrow{OM}=\overrightarrow{CT}=\overrightarrow{DB}\Leftrightarrow \overrightarrow{OM}=\frac{1}{2}\overrightarrow{DB}\)
Lấy $K$ là trung điểm của $BB'$
Vì $O$ là tâm hình hộp nên $O$ là trung điểm $B'D$
\(\Rightarrow OK\parallel BD; OK=\frac{1}{2}BD\)
\(\Rightarrow \overrightarrow{OK}=\frac{1}{2}{DB}\)
Do đó \(K\equiv M\) hay M là trung điểm của $BB'$


\(A'C'||AC\Rightarrow\) góc cần tìm là góc \(\widehat{CAB'}\)
Mặt khác \(AB'=AC=B'C\) (các đường chéo của hình vuông bằng nhau)
\(\Rightarrow\Delta AB'C\) đều
\(\Rightarrow\widehat{CAB'}=60^0\)