Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
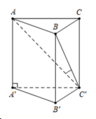
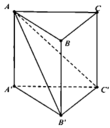
Ta có A A ' ⊥ A B A C ⊥ A B ⇒ A B ⊥ A C C ' A ' ⇒ B C ' ; A C C ' A ' ^ = B C ' A ^
Tam giác B A C ' vuông tại A, có tan B C ' A ^ = A B A C ' ⇒ A C ' = a 3 tan 30 0 = 3 a
Tam giác A A ' C ' vuông tại A' , có A A ' = A C ' 2 − A ' C ' 2 = 2 a 2
Thể tích khối lăng trụ cần tính là V = A A ' . S A B C = 2 a 2 . 1 2 . a 3 a = a 3 6

Đáp án D
Phương pháp :
+) Kẻ AD ⊥ B’C, xác định góc giữa mặt phẳng (AB’C) và mặt phẳng (BCC’B’)
+) Tính BB’.
+) Tính thể tích khối lăng trụ và suy ra thế tích AB’CA’C’
Cách giải :
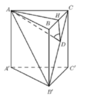
Gọi H là trung điểm của BC ta có
![]()
Trong (AB’C) kẻ AD ⊥ B’C
![]()
Ta có:

=> ((AB'C);(BCC'B')) = (AD;HD) = ADH
Ta có 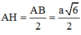

Dễ thấy ∆CBB’ đồng dạng với ∆CDH (g.g)
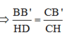
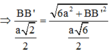
![]()
![]()
Ta có: 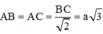
![]()
![]()
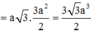
![]()
![]()

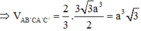

Đáp án A.
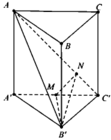
Dựng B ' M ⊥ A ' C ' ⇒ B ' M ⊥ A C C ' A '
Dựng M N ⊥ A C ' ⇒ A C ' ⊥ M N B '
Khi đó A B ' C ' ; A C ' A ' ^ = M N B ' ^ = 60 0
Ta có:
B ' M = a 2 2 ⇒ M N = B ' M tan M N B ' ^ = a 6 6
Mặt khác tan A C ' A ' ^ = M N C ' N = AA ' A ' C '
Trong đó:
M N = a 6 6 ; M C ' = a 2 2 ⇒ C ' N = C ' M 2 − M N 2 = a 3 3
Suy ra AA ' = a
Thể tích lăng trụ:
V = A B 2 2 . h = a 3 2 ⇒ V B ' . A C C ' A ' = V − V B ' . B A C = V − V 3 = 2 3 V = a 3 3 .

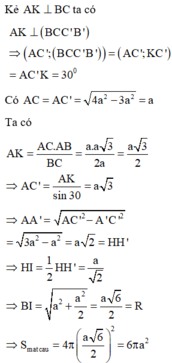


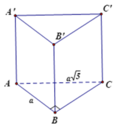

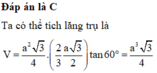

Chọn đáp án B.