Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Phương pháp:

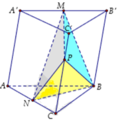
+) So sánh diện tích hình thang BMNC và diện tích hình bình hành BCC’B’ từ đó suy ra tỉ số thể tích V A . B M N C V A . B C C ' B '
+) So sánh V A . B C C ' B ' với V.
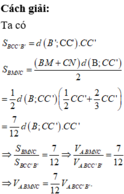
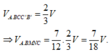

Đáp án C
Ta có V A B C . M N P V A B C . A ' B ' C ' = A M A A ' + B N B B ' + C P C C ' 3 = 1 2 + 2 . 2 3 3 = 11 18 → V A B C . M N P = 11 18 6 a 3 = 11 3 a 3 .

Đáp án A
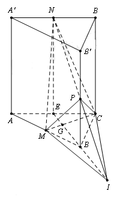
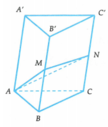
Gọi E là trung điểm của A C ⇒ N E / / B B ' . Nối NP cắt BE tại I suy ra B là trung điểm của EI. Gọi G là trọng tâm của tam giác ABC ⇒ B G = 2 E G .
⇒ d B ; M C = 2 d E ; M C ⇒ d B ; M C = 2 3 d B ; A C
Suy ra: d I ; M C = 1 + 3 2 d B ; M C = 5 2 d B ; M C
Mà S Δ I M C = 1 2 d I ; M C . M C
= 1 2 . 5 2 d B ; M C . M C = 5 2 S Δ M B C = 5 4 S Δ A B C
Ta có: V N . M P C V N . M I C = N P N I = 1 2 ⇒ V N . M P C = 1 2 x V N . M I C 1
Lại có:
V N . M I C = 1 3 . d N ; A B C . S Δ I M C = 1 3 . d A ' ; A B C . 5 4 S Δ A B C ⇒ V N . M I C = 5 12 . d A ' ; A B C . S Δ A B C = 5 12 V A B C . A ' B ' C ' = 5 12 V
Từ (1) và (2) suy ra V C M N P = 1 2 . 5 12 x V = 5 24 V .
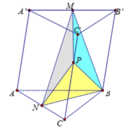

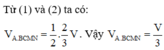
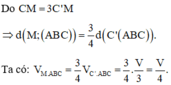

Đáp án B