Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Dễ thấy BD ⊥ SC, nên BD // (AB'C'D'), suy ra BD // B'D'.
Gọi I = AC ∩ BD, J = AC' ∩ SI, khi đó J là trọng tâm của tam giác SAC và J ∈ B'D'.
Suy ra
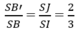
Do đó dễ thấy
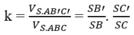

Gọi O là giao điểm của AC và BD. Dễ thấy \(\Delta OAB\) vuông tại O và \(OB=\dfrac{a\sqrt{3}}{2}\). Từ đó \(OA=\sqrt{AB^2-OB^2}=\sqrt{\left(\dfrac{\sqrt{3}}{2}a\right)^2-a^2}=\sqrt{\dfrac{1}{4}a^2}=\dfrac{a}{2}\) \(\Rightarrow AC=a\).
Vì \(SA\perp mp\left(ABCD\right)\) nên \(SA\perp AC\) tại A hay \(\Delta SAC\) vuông tại A.
Lại có \(\tan SAC=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\) nên \(\widehat{SAC}=60^o\), suy ra góc giữa SC và mp(ABCD) bằng 60o \(\Rightarrow\) Chọn A
Chỗ \(\widehat{SAC}\) em sửa lại là \(\widehat{SCA}\) mới đúng ạ.

\(AC=AB\sqrt{2}=4a\)
Áp dụng định lý Pitago:
\(CC'=\sqrt{\left(AC'\right)^2-AC^2}=3a\)
\(\Rightarrow V=3a.\left(2a\sqrt{2}\right)^2=24a^3\)

Chọn A.
(h.2.59) Trong tam giác ABC vuông tại A, ta có:
AC = BC.sin30 ° = a;
AB = BC.cos30 ° = a 3 .
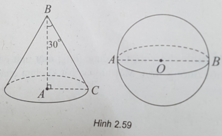
Diện tích toàn phần hình nón là:
S 1 = S xq + S đáy = πRl + πR 2 = πa . 2 a + πa 2 = 3 πa 2
Diện mặt cầu đường kính AB là:
S 2 = πAB 2 = π a 3 2 = 3 πa 2
Từ đó suy ra, tỉ số S 1 / S 2 = 1

Chọn D.
Gọi H là trung điểm của cạnh AD. Kẻ HI vuông góc với A'D tại I. Khi đó d(B,(A'DCB')) = d(A,(A'DCB')) = 2d(H,(A'DCB')) = 2HI.


Đáp án C
Hình chiếu vuông góc của D xuống mặt phẳng ( B C B 1 C 1 ) là điểm C. Theo đề bài, ta có D B 1 C ^ = 30 o
Do đó