Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

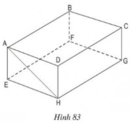
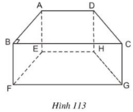
a) BC // FG ⇒ BC // (EFGH)
CD // HG ⇒ CD // (EFGH)
AD // EH ⇒ AD // (EFGH)
Vậy: ngoài AB, các cạnh song song với mặt phẳng (EFGH) là BC, CD, AD
b) CD // AB ⇒ CD // (ABFE)
và CD // (EFGH) ( theo ý a).
c) Vì AB // HG, AB = HG ⇒ ABGH là hình bình hành
⇒ AH // BG
⇒ AH // (BCGF)
Vậy mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).

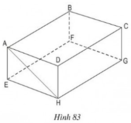
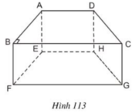
a) BC // FG ⇒ BC // (EFGH)
CD // HG ⇒ CD // (EFGH)
AD // EH ⇒ AD // (EFGH)
Vậy: ngoài AB, các cạnh song song với mặt phẳng (EFGH) là BC, CD, AD
b) CD // AB ⇒ CD // (ABFE)
và CD // (EFGH) ( theo ý a).
c) Vì AB // HG, AB = HG ⇒ ABGH là hình bình hành
⇒ AH // BG
⇒ AH // (BCGF)
Vậy mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).

a) Những đường thẳng song song với mặt phẳng (EFGH) là: AB; BC; CD; DA.
b) Đường thẳng AB song song với những mặt phẳng: (CDHG); (EFGH); (DCFE)
c) Đường thẳng AD song song với những đường thẳng: BC, FG, EH

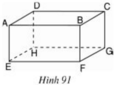
a) Các cạnh song song với cạnh AD là EH, BC, FG.
b) Các cạnh song song với cạnh AB là EF.
c) Các đường thẳng song song với mặt phẳng (EFGH) là: AD, BC, AB, CD.
d) Các đường thẳng song song với mặt phẳng (DCGH): AE, BF.

a) Các cạnh song song với cạnh AD là EH, BC, FG.
b) Các cạnh song song với cạnh AB là EF.
c) Các đường thẳng song song với mặt phẳng (EFGH) là: AD, BC, AB, CD.
d) Các đường thẳng song song với mặt phẳng (DCGH): AE, BF.

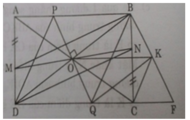
d) Gọi F là giao điểm của BK và QC. Ta có O là trung điểm của BD và OQ // BK (gt) nên Q là trung điểm của DF.
Lại có QK // BD (gt); Q là trung điểm của DF ⇒ K là trung điểm của BF.
CK là trung tuyến của tam giác vuông BCF ⇒ CK = BK = BC/2.
Ta có QK là đường trung bình của tam giác
⇒ QK = BO = BD/2; QK // BO
⇒ Tứ giác OBKQ là hình bình hành
Mặt khác ∠(OBQ) = 90o ⇒ OBKQ là hình chữ nhật
⇒ ∠(OBK) = 90o
Xét ΔOCK và ΔOBK có
CK chung
OC = OB (tính chất đường chéo hình chéo hình chữ nhật)
CK = BK (cmt)
Vậy ΔOCK = ΔOBK (c.c.c) ⇒ ∠OCK = ∠OBK = 90o hay AC ⊥ CK.


a) \(\left\{{}\begin{matrix}mp\left(ABCD\right):AB=CD\left(1\right)\\mp\left(ABB'A'\right):AB=A'B'\left(2\right)\\mp\left(CDD'C'\right):CD=C'D'\left(3\right)\\mp\left(A'B'C'D'\right):A'B'=C'D'\left(4\right)\end{matrix}\right.-\text{Tính chất hình chữ nhật}\)
Từ (1) và (3) => \(AB=CD=C'D'\) (*)
Từ (2) và (4) => \(AB=A'B'=C'D'\) (**)
Vậy từ(*) và (**) suy ra : \(AB=CD=C'D'=A'B'\)
b) \(C'D'//CD\Leftrightarrow\left\{{}\begin{matrix}C'D'\in mp\left(CDD'C'\right)\\CD\in\left(CDD'C'\right)\\\text{Không có điểm chung}\end{matrix}\right.\)
c) * \(AD//mp\left(BCC'B'\right)\) vì :
\(\left\{{}\begin{matrix}AD\notin mp\left(BCC'B'\right)\\AD//BC\end{matrix}\right.\)
* \(AD//mp\left(A'B'C'D'\right)\) vì :
\(\left\{{}\begin{matrix}AD\notin mp\left(A'B'C'D'\right)\\AD//A'D'\end{matrix}\right.\)
d) \(mp\left(ADD'A'\right)//mp\left(BCC'B'\right)\)



Câu C đúng nha bạn