Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tương tự 1A
a) AB' và C'D song song, B'D' và AD chéo nhau, AC và A'C' song song.
b) BC' song song với (ADD'A').
c) AC' và CA' cắt nhau tại C.
d) (ACC'A') và (BDD'B') cắt nhau theo giao tuyến OO' (O và O' lần lượt là giao của AC, BD và A'C', B'D')
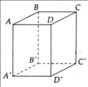

Lời giải:
a)
Vì $ABCD$ là hình thoi nên hai đường chéo $AC$ và $BD$ vuông góc với nhau
\(\Rightarrow \angle DOC=90^0\)
Ta có:
\(\left\{\begin{matrix} DE\parallel AC\\ AC\perp BD\end{matrix}\right.\Rightarrow DE\perp BD\Rightarrow \angle EDB=90^0\)
\(\left\{\begin{matrix} CE\parallel BD\\ BD\perp AC\end{matrix}\right.\Rightarrow CE\perp AC\Rightarrow \angle OCE=90^0\)
Xét tứ giác $ODEC$ có 3 góc đều là góc vuông nên là hình chữ nhật (đpcm)
b) Vì $ODEC$ là hình chữ nhật nên hai đường chéo $CD$ và $OE$ bằng nhau (\(OE=CD)\)
Mà $ABCD$ là hình thoi nên $BC=CD$
\(\Rightarrow OE=BC\) (đpcm)

Giải
a) Tứ giác ABA'B' có OB = OB' ; OA = OA'
Tức là hai đường chéo cắt nhau tại trung điểm O của mỗi đường nên ABA'B' là hình bình hành
Vậy A'B' // AB (hình bình hành có các cạnh đối song song với nhau)
b) Tương tự câu a, ta có: A'B // AB'
a) \(\left\{{}\begin{matrix}mp\left(ABCD\right):AB//CD\\mp\left(CDD'C'\right):CD//C'D'\end{matrix}\right.\left(\text{Tính chất hình chữ nhật}\right)\)
\(\Rightarrow AB//C'D'\left(\text{Cùng song song với CD}\right)\)
b) \(\left\{{}\begin{matrix}mp\left(ABCD\right):AD//BC\\mp\left(BCC'B'\right):BC//B'C'\end{matrix}\right.\left(\text{Tính chất hình chữ nhật}\right)\)
\(\Rightarrow AD//B'C'\left(\text{Cùng song song với BC}\right)\)
c) \(\left\{{}\begin{matrix}mp\left(ADD'A'\right):AA'//DD'\\mp\left(CDD'C'\right):CC'//DD'\end{matrix}\right.\left(\text{Tính chất hình chữ nhât}\right)\)
\(\Rightarrow AA'//CC'\) (Cùng song song với DD')