Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có hai trường hợp xảy ra:
Trường hợp 1:
(P) đi qua A, song song với hai đường thẳng d và BC. Vectơ chỉ phương của d là v → (-3; -1; 2) và BC → (-2; 4; 0).
Do đó n P → = v → ∧ BC → = (-8; -4; -14).
Phương trình mặt phẳng (P) là: -8(x - 1) - 4(y - 2) - 14(z - 1) = 0 hay 4x + 2y + 7z - 15 = 0
Trường hợp 2:
(P) đi qua A, đi qua trung điểm F(1; 1; 1) của BC, và song song với d.
Ta có: FA → (0; 1; 0), FA → ∧ v → = (2; 0; 3).
Suy ra phương trình của (P) là: 2(x - 1) + 3(z - 1) = 0 hay 2x + 3z - 5 = 0.

Chọn D.
Gọi H là trung điểm của cạnh AD. Kẻ HI vuông góc với A'D tại I. Khi đó d(B,(A'DCB')) = d(A,(A'DCB')) = 2d(H,(A'DCB')) = 2HI.

Chọn D
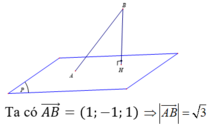
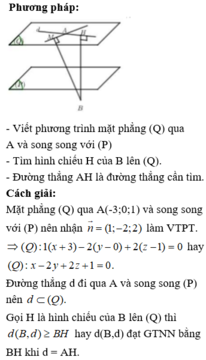
Gọi H là hình chiếu của B trên mặt phẳng (P) khi đó ta có BH là khoảng cách từ điểm B đến mặt phẳng (P). Ta luôn có BH ≤ AB do đó khoảng cách từ B đến mặt phẳng (P) lớn nhất khi H ≡ A, khi đó ![]() là véc tơ pháp tuyến của mặt phẳng (P)
là véc tơ pháp tuyến của mặt phẳng (P)
Vậy phương trình mặt phẳng (P) đi qua A (-1; 2; 4) và có véc tơ pháp tuyến ![]() là x - y + z - 1 = 0
là x - y + z - 1 = 0
Vậy khoảng cách từ điểm O đến mặt phẳng (P) là:
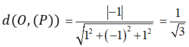

\(\left\{{}\begin{matrix}a+8-c+d=0\\\dfrac{\left|a-8+2c+d\right|}{\sqrt{a^2+16+c^2}}=5\end{matrix}\right.\)
\(\Rightarrow\left(3c-16\right)^2=25\left(a^2+c^2+16\right)\)
\(\Rightarrow25a^2+16c^2+96c+144=0\)
\(\Rightarrow25a^2+16\left(c+3\right)^2=0\Rightarrow\left\{{}\begin{matrix}a=0\\c=-3\end{matrix}\right.\)
\(\Rightarrow d=c-a-8=-11\)
\(\Rightarrow a+c+d=-14\)

Đáp án B
Cách giải:
![]()
d : x - 2 1 = y - 1 - 2 = z - 1 2 có 1 VTCP v → =(1;-2;2) là một VTCP của ∆
∆ là đường thẳng qua A, vuông góc với d ⇒ ∆ ⊂ ( α ) mặt phẳng qua A và vuông góc d mặt phẳng qua A và vuông góc d
Phương trình mặt phẳng α
![]()
![]()
![]()
khi và chỉ khi đi qua hình chiếu H của B lên α
*) Tìm tọa độ điểm H:
Đường thẳng BH đi qua B(2;0;4) và có VTCP là VTPT của α có phương trình:
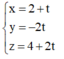
![]()
![]()
![]()
![]()
![]()
![]()

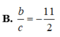
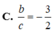
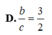
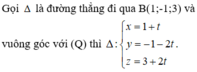
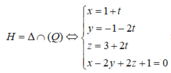
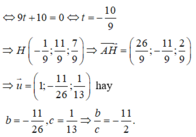


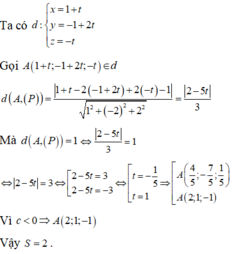

Đáp án: C