Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
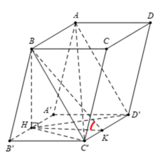
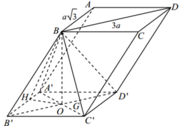
Gọi H là trung điểm của BC, kẻ H K ⊥ C ' D ' K ∈ C ' D '
Suy ra B H ⊥ A ' B ' C ' D ' ⇒ A C ' D ' ; A ' B ' C ' D ' ^ = B K H ^
Tam giác A’C’D’ đều cạnh 2 a ⇒ H K = d A ' ; C ' D ' = a 3
Tam giác BHK vuông tại H ⇒ B H = tan 60 ∘ x H K = 3 a
Diện tích hình thoi A’B’C’D’ là S A ' B ' C ' D ' = 2 a 2 3 .
Vậy thể tích khối lăng trụ ABC.A’B’C’D’ là V = B H . S A ' B ' C ' D ' = 3 a .2 a 2 3 = 6 3 a 3

Đáp án D
Phương pháp:
Thể tích hình hộp trong đó:
B: diện tích đáy,
h: chiều cao
Cách giải:
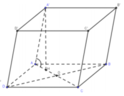
Do AA’ // CC’ nên (AA’,ABCD) = (CC’,ABCD) = 600
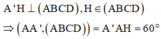
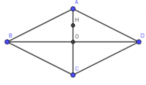
Hình thoi ABCD có AB = CD = BC = DA = a. BD= B'D' = a 3
Tam giác OAB vuông tại O:
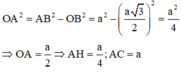
Diện tích hình thoi ABCD: 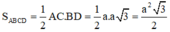
Tam giác A’AH vuông tại H:
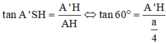
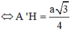
Thể tích hình hộp ABCD.A’B’C’D’:
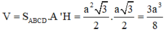

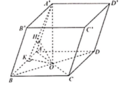
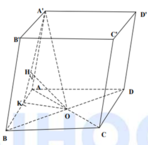
Gọi O = A C ∩ B D
Từ giả thuyết suy ra A ' O ⊥ A B C D
Ta có S A B C D = B C . C D . sin 120 o = a 2 3 2
Vì B C D ^ = 120 o nên A B C ^ = 60 o
Suy ra ∆ A B C đều
⇒ A C = a ⇒ A ' O = A ' A 2 - A O 2 = 49 a 2 4 - a 2 4 = 2 3 a
Vậy V A B C D . A ' B ' C ' D ' = 3 a 3
Đáp án B
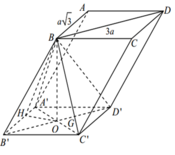
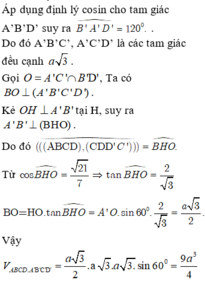

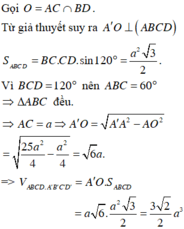
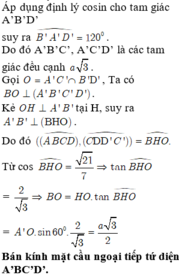

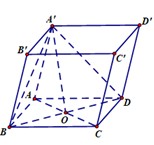

Đáp án là C