Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi G là trọng tâm tam giác \(\Rightarrow\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=0\)
\(\overrightarrow{MA}^2+\overrightarrow{MA}.\overrightarrow{MB}+\overrightarrow{MA}.\overrightarrow{MC}=0\)
\(\Leftrightarrow\overrightarrow{MA}\left(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right)=0\)
\(\Leftrightarrow\overrightarrow{MA}\left(\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right)=0\)
\(\Leftrightarrow3\overrightarrow{MA}.\overrightarrow{MG}=0\)
\(\Rightarrow\) M thuộc đường tròn đường kính AG
Bán kính: \(R=\dfrac{1}{2}AG=\dfrac{1}{2}.\dfrac{2}{3}.\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{3}}{6}\)

a.
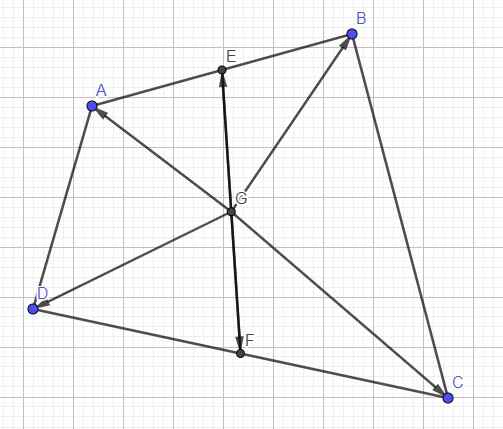
E và F là trung điểm AB và CD nên: \(\overrightarrow{AB}=2\overrightarrow{AE}\) ; \(\overrightarrow{DC}=2\overrightarrow{DF}\)
G là trung điểm EF nên: \(\overrightarrow{AE}+\overrightarrow{AF}=2\overrightarrow{AG}\)
Do đó:
\(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=2\overrightarrow{AE}+\overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{AD}=2\overrightarrow{AE}+2\overrightarrow{AD}+2\overrightarrow{DF}\)
\(=2\overrightarrow{AE}+2\left(\overrightarrow{AD}+\overrightarrow{DF}\right)=2\overrightarrow{AE}+2\overrightarrow{AF}=2\left(\overrightarrow{AE}+\overrightarrow{AF}\right)=4\overrightarrow{AG}\)
b.
\(\left(\overrightarrow{GA}+\overrightarrow{GB}\right)+\left(\overrightarrow{GC}+\overrightarrow{GD}\right)=2\overrightarrow{GE}+2\overrightarrow{GF}=2\left(\overrightarrow{GE}+\overrightarrow{GF}\right)=2.\overrightarrow{0}=\overrightarrow{0}\)
c.
Từ câu b ta có:
\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}\)
\(\Rightarrow\overrightarrow{GO}+\overrightarrow{OA}+\overrightarrow{OG}+\overrightarrow{OB}+\overrightarrow{GO}+\overrightarrow{OC}+\overrightarrow{GO}+\overrightarrow{OD}=\overrightarrow{0}\)
\(\Rightarrow4\overrightarrow{GO}+\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}\)
\(\Rightarrow4\overrightarrow{OG}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}\)
\(\Rightarrow\overrightarrow{OG}=\dfrac{1}{4}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}\right)\)

Lời giải:
a)
$2\overrightarrow{AD}=\overrightarrow{AD}+\overrightarrow{AD}$
$=\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{AC}+\overrightarrow{CD}$
$=\overrightarrow{AB}+\overrightarrow{AC}+(\overrightarrow{BD}+\overrightarrow{CD})$
$=\overrightarrow{AB}+\overrightarrow{AC}$
$\Rightarrow \overrightarrow{AD}=\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}$
Tương tự:
$\overrightarrow{BE}=\frac{\overrightarrow{BC}+\overrightarrow{BA}}{2}$
$\overrightarrow{CF}=\frac{\overrightarrow{CA}+\overrightarrow{CB}}{2}$
Cộng lại:
$\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\frac{\overrightarrow{AB}+\overrightarrow{BA}+\overrightarrow{AC}+\overrightarrow{CA}+\overrightarrow{BC}+\overrightarrow{CB}}{2}=\frac{\overrightarrow{0}+\overrightarrow{0}+\overrightarrow{0}}{2}=\overrightarrow{0$}$
Ta có đpcm.
b)
$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{MD}+\overrightarrow{DA}+\overrightarrow{ME}+\overrightarrow{EB}+\overrightarrow{MF}+\overrightarrow{FC}$
$=(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF})+(\overrightarrow{DA}+\overrightarrow{EB}+\overrightarrow{FC})$
$=(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF})-(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF})$
$=\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}-\overrightarrow{0}$ (theo phần a)
$=\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}$
Ta có đpcm.

Gọi \(M\left(m;0\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(1-m;1\right)\\\overrightarrow{MB}=\left(-2-m;4\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{MA}-2\overrightarrow{MB}=\left(m+5;-7\right)\)
\(\Rightarrow\left|\overrightarrow{MA}-2\overrightarrow{MB}\right|=\sqrt{\left(m+5\right)^2+49}\ge7\)
Dấu "=" xảy ra khi \(m+5=0\Leftrightarrow m=-5\) hay \(M\left(-5;0\right)\)

\(\overrightarrow{AM}.\overrightarrow{AB}=AM^2=\overrightarrow{AM}^2\)
\(\Leftrightarrow\overrightarrow{AM}\left(\overrightarrow{AB}-\overrightarrow{AM}\right)=0\)
\(\Rightarrow\overrightarrow{AM}.\overrightarrow{MB}=0\)
\(\Rightarrow AM\perp BM\)
\(\Rightarrow\) Quỹ tích là đường tròn đường kính AB
Hình bạn tự vẽ :
MA+MB+MC+MD=4MO
( Chèn điểm O)
VT= MO+OA+MO+OB+MO+OC+MO+OD
=4MO+(OA+OB+OC+OD)
= 4MO+ 0
= 4MO=VP(dpcm)