Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Để \(AC\perp BD\) thì \(\Rightarrow\overrightarrow{AC}\cdot\overrightarrow{BD}=0\Rightarrow\left(\overrightarrow{AB}+\overrightarrow{BC}\right)\left(\overrightarrow{BA}+\overrightarrow{AD}\right)=0\\ \Rightarrow\overrightarrow{AB}\cdot\overrightarrow{BA}+\overrightarrow{BC}\cdot\overrightarrow{BA}+\overrightarrow{AB}\cdot\overrightarrow{AD}+\overrightarrow{BC}\cdot\overrightarrow{AD}=0\\ \Rightarrow-h^2+0+0+ab=0\\ \Rightarrow h^2=ab\)
b) Để \(AI\perp BI\) thì \(\Rightarrow\overrightarrow{AI}\cdot\overrightarrow{BI}=0\Rightarrow\dfrac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{AC}\right)\dfrac{1}{2}\left(\overrightarrow{BD}+\overrightarrow{BC}\right)=0\\ \Rightarrow\left(\overrightarrow{AD}+\overrightarrow{AB}+\overrightarrow{BC}\right)\left(\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{BC}\right)=0\\ \\ \Rightarrow\overrightarrow{AD}\cdot\overrightarrow{BA}+\overrightarrow{AB}\cdot\overrightarrow{BA}+\overrightarrow{BC}\cdot\overrightarrow{BA}+\overrightarrow{AD}\cdot\overrightarrow{AD}+\overrightarrow{AB}\cdot\overrightarrow{AD}+\overrightarrow{BC}\cdot\overrightarrow{AD}+\overrightarrow{AD}\cdot\overrightarrow{BC}+\overrightarrow{AB}\cdot\overrightarrow{BC}+\overrightarrow{BC}\cdot\overrightarrow{BC}=0\\ \Rightarrow-h^2+a^2+ab+ab+b^2=0\\ \Rightarrow a^2+2ab+b^2=\left(a+b\right)^2=h^2\\ \Rightarrow a+b=h\)

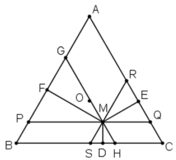
Ta có:
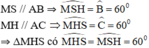
⇒ ΔMHS đều.
MD ⊥ SH nên MD là đường cao đồng thời là trung tuyến của ΔMHS.
⇒ D là trung điểm của HS
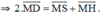
Chứng minh tương tự ta có:
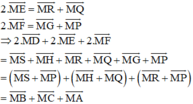
(Vì các tứ giác BSMP, HMQC, MRAG là hình bình hành)