Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


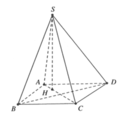
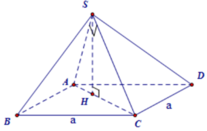
Vẽ S H ⊥ A C tại H.
Khi đó: ( S A C ) ⊥ ( A B C D ) ( S A C ) ⊥ ( A B C D ) = A C S H ⊂ ( S A C ) S H ⊥ A C
⇒ S H ⊥ ( A B C D ) ⇒ V = 1 3 S H . S A B C D
Theo đề ∆ S A C vuông tại S nên ta có:
S C = A C 2 - S A 2 = 6 a 2
và S H = S A . S C A C
= 2 a 2 . 6 a 2 2 a = 6 a 4
Vậy V = 1 3 S H . S A B C D = 6 a 3 12
Chọn đáp án A.

Đáp án A
V SABCD = 1 3 . S ABCD . d S , ABCD = 1 3 . a 2 . d S , ABCD = 3 a 3 ⇒ d S , ABCD = 9 a .

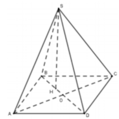
Gọi H là trọng tâm tam giác ABC. Vì S.ABC là tứ diện đều cạnh a nên S H ⊥ A B C hay S H ⊥ A B C D v à S A = S B = S C = A C = B C = a
Gọi O là giao điểm hai đường chéo hình thoi ABCD thì B H = 2 3 B O
Vì ABC đều có BO là trung tuyến nên \ B O = a 3 2

Xét tam giác SBH vuông tại H ta có

Diện tích hình thoi ABCD là
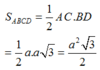
Thể tích khối chóp S.ABCD là
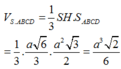 .
.
Chọn B.
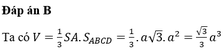
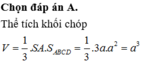

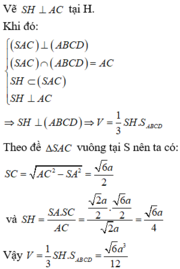
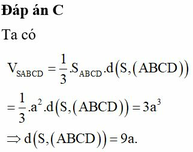
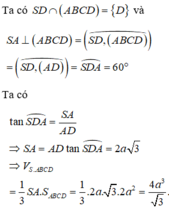
Phương pháp
Công thức tính thể tích khối chóp có diện tích đáy S và chiều cao h là: