Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
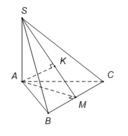
Gọi M là trung điểm BC
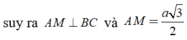
Gọi K là hình chiếu của A trên SM , suy ra AK ⊥ SM. (1)
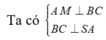
![]()
![]()
![]()
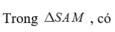
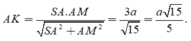
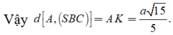

Chọn C.
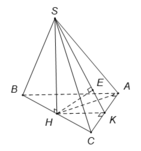
Gọi H là trung điểm của BC, suy ra .
![]()
Gọi K là trung điểm AC
![]()
![]()
![]()
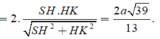

Gọi H là trung điểm AD \(\Rightarrow SH\perp\left(ABCD\right)\) và \(SH=\dfrac{a\sqrt{3}}{2}\)
Gọi M là trung điểm BC \(\Rightarrow HM||CD\Rightarrow HM\perp CB\) đồng thời \(HM=CD=a\)
\(\Rightarrow BC\perp\left(SHM\right)\)
Trong mp (SHM), từ H kẻ \(HK\perp SM\Rightarrow HK\perp\left(SBC\right)\)
\(\Rightarrow HK=d\left(H;\left(SBC\right)\right)\)
\(\dfrac{1}{HK^2}=\dfrac{1}{SH^2}+\dfrac{1}{HM^2}\Rightarrow HK=\dfrac{SH.HM}{\sqrt{SH^2+HM^2}}=\dfrac{a\sqrt{21}}{7}\)
\(DH||BC\Rightarrow DH||\left(SBC\right)\Rightarrow d\left(D;\left(SBC\right)\right)=d\left(H;\left(SBC\right)\right)=\dfrac{a\sqrt{21}}{7}\)

Tam giác SBC cân hay đều em nhỉ?
Vì tam giác SBC đều thì sẽ không khớp với dữ kiện \(V_{SABC}=\dfrac{a^3}{16}\)

Chọn D
Phương pháp:
Xác định khoảng cách sau đó dùng công thức hệ thức lượng trong tam giác vuông để tính khoảng cách đó.
Cách giải:
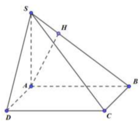
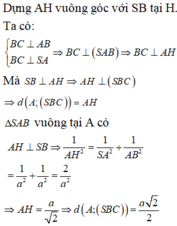

Đáp án B
HDG:
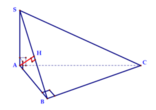
![]()
Dễ dàng chứng minh ∆ S B C vuông tại B
![]()
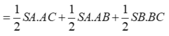
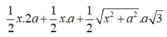
![]()
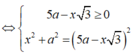
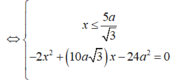
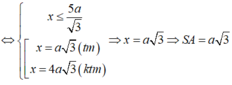
Ta có (SAB) ⊥ (SBC) theo giao tuyến SB. Kẻ
![]()
![]()

Đáp án D

Gọi H, I , theo thứ tự là trung điểm AD,BC
G là tâm đường tròn nội tiếp tam giác đều
SAD nên G cũng là trọng tâm tam giác SAD.
![]()
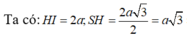

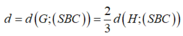
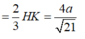

Chọn A
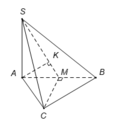
Xác định được
![]()
![]()
Do M là trung điểm của cạnh AB nên
![]()
![]()
![]()
Tam giác vuông SAM có
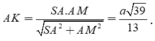
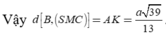
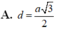
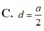
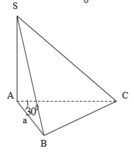
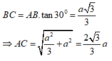
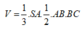
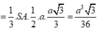
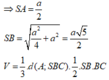
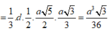
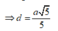
Đáp án C