Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Phương pháp:
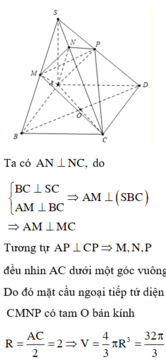
+ Chứng minh: O là tâm mặt cầu ngoại tiếp tứ diện CMNP (với O là tâm của hình vuông ABCD)
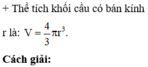



Đáp án C
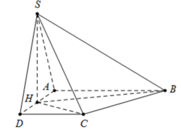
Tam giác SAD đều cạnh 2 a ⇒ S H = a 3 ⇒ H C − 2 a 3 .
Kẻ BK vuông góc H C ⇒ B K ⊥ S H C ⇒ B K − 2 a 6
Diện tích tam giác BHC là S Δ B H C = 1 2 B K . H C = 6 a 2 2
Mà S A B C D = S Δ H A B + S Δ H C D + S Δ H B C = 1 2 S A B C D + S Δ H B C ⇒ S A B C D = 2 x S Δ H B C = 12 a 2 2
V S . A B C D = 1 3 . S H . S Δ H B C = 1 3 . a 3 .12 a 2 2 = 4 6 a 3


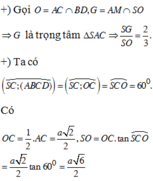

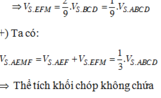
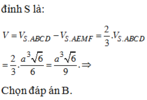
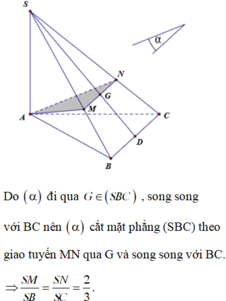

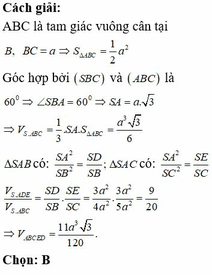

Đáp án B
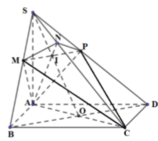
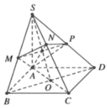
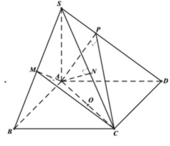
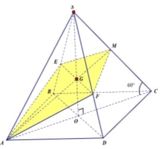
Nối S O ∩ A N = E , qua E kẻ đường thẳng song song với BD. Cắt SB,SD lần lượt tại M , P ⇒ m p P ≡ A M N P .
Ta có S A ⊥ A B , S A ⊥ A D ⇒ S A ⊥ A B C D ⇒ B C ⊥ S A B .
Mà SC ⊥ A M N P ⇒ S C ⊥ A M suy ra A M ⊥ S B C .
Do đó A M ⊥ M C mà O là trung điểm của A C ⇒ O A = O M = O C .
Tương tự, ta chứng minh được O là tâm mặt cầu ngoại tiếp khối
đa diện A B C D . M N P ⇒ R = A C 2 = 4 a 3 2 = 2 a 3 .
Vậy thể tích cần tính là V = 4 3 π R 3 = 4 3 π 2 3 3 = 32 3 π a 3 .