Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

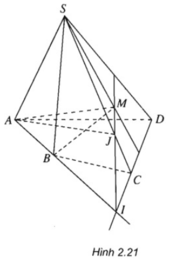
a) Ta có ngay S, M là hai điểm chung của (SBM) và (SCD) nên (SBM) ∩ (SCD) = SM
b) M là điểm chung thứ nhất của (AMB) và (SCD)
Gọi I = AB ∩ CD
Ta có: I ∈ AB ⇒ I ∈ (ABM)
Mặt khác: I ∈ CD ⇒ I ∈ (SCD)
Nên (AMB) ∩ (SCD) = IM.
c) Gọi J = IM ∩ SC.
Ta có: J ∈ SC ⇒ J ∈ (SAC) và J ∈ IM ⇒ J ∈ (ABM).
Hiển nhiên A ∈ (SAC) và A ∈ (ABM)
Vậy (SAC) ∩ (ABM) = AJ

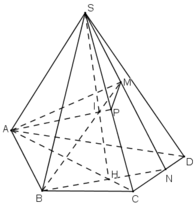
a) SM, CD cùng thuộc (SCD) và không song song.
Gọi N là giao điểm của SM và CD.
⇒ N ∈ CD và N ∈ SM
Mà SM ⊂ (SMB)
⇒ N ∈ (SMB)
⇒ N = (SMB) ∩ CD.
b) N ∈ CD ⊂ (ABCD)
⇒ BN ⊂ (ABCD)
⇒ AC; BN cùng nằm trong (ABCD) và không song song
Gọi giao điểm của AC và BN là H.
+ H ∈ AC ⊂ (SAC)
+ H ∈ BN ⊂ (SBM)
⇒ H ∈ (SAC) ∩ (SBM)
Dễ dàng nhận thấy giao điểm thứ hai của (SAC) và (SBM) là S
⇒ (SAC) ∩ (SBM) = SH.
c) Trong mp(SBM), gọi giao điểm của BM và SH là I, ta có:
I ∈ BM
I ∈ SH ⊂ (SAC).
⇒ I = BM ∩ (SAC).
) Trong mp(SAC), gọi giao điểm của AI và SC là P.
+ P ∈ AI, mà AI ⊂ (AMB) ⇒ P ∈ (AMB)
⇒ P = (AMB) ∩ SC.
Lại có P ∈ SC, mà SC ⊂ (SCD) ⇒ P ∈ (SCD).
⇒ P ∈ (AMB) ∩ (SCD).
Lại có: M ∈ (SCD) (gt)
⇒ M ∈ (MAB) ∩ (SCD)
Vậy giao điểm của (MAB) và (SCD) là đường thẳng MP.

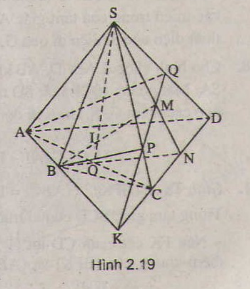
a) Trong (SCD) kéo dài SM cắt CD tại N, Chứng minh N thuộc (SBM)
b) (SBM) ≡ (SBN). Giao tuyến cần tìm là SO
c) Trong (SBN) ta có MB giao SO tại I
d) Trong (ABCD) , ta có AB giao CD tại K, Trong (SCD), ta có KQ giao SC tại P
Từ đó suy ra được giao tuyến của hai mặt phẳng (SCD) và (ABM) là KQ.

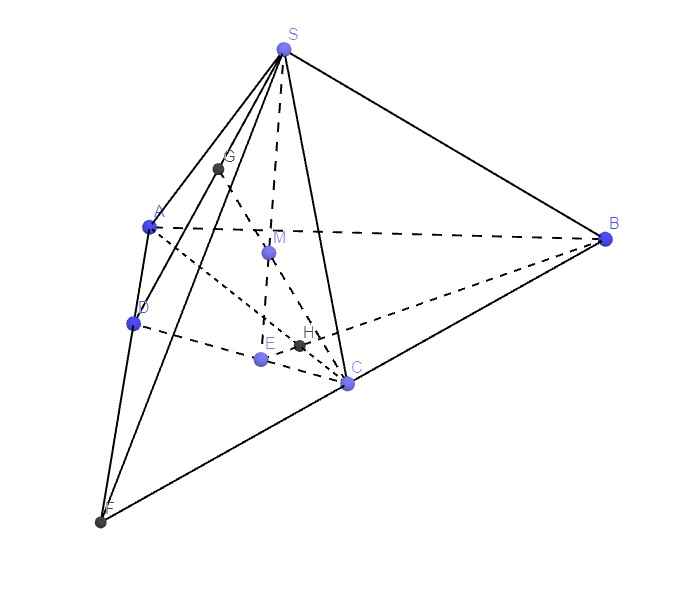
Nối BC và AD kéo dài cắt nhau tại F
\(\Rightarrow SF=\left(SBC\right)\cap\left(SAD\right)\)
Trong mp (SCD), nối CM kéo dài cắt SD tại G
\(\Rightarrow AG=\left(AMC\right)\cap\left(SAD\right)\)
Trong mp (SCD), nối SM kéo dài cắt CD tại E
\(\Rightarrow AE=\left(SAM\right)\cap\left(ABCD\right)\)
Trong mp (ABCD), nối BE cắt AC tại H
\(\Rightarrow SH=\left(SBM\right)\cap\left(SAC\right)\)

a/ Kéo dài SM cắt CD ở N
\(\left(SBM\right)\equiv\left(SBN\right)\)
\(\left(SBN\right)\cap\left(ABCD\right)=BN\)
\(BN\cap CD=\left\{N\right\}\Rightarrow CD\cap\left(SBM\right)=\left\{N\right\}\)
b/ Tương tự như câu a, ta sẽ tiếp tục sử dụng (SNB) bởi (SNB)=(SMB)
\(AC\cap BN=\left\{H\right\}\Rightarrow H=\left(SAC\right)\cap\left(SBN\right)\)
\(\Rightarrow\left(SAC\right)\cap\left(SBN\right)=SH\Rightarrow\left(SAC\right)\cap\left(SBM\right)=SH\)
c/ \(SH\cap BM=\left\{I\right\}\Rightarrow I=BM\cap\left(SAC\right)\)
d/ \(SC\subset\left(SCD\right)\)
\(AB\cap CD=\left\{K\right\}\Rightarrow\left(ABM\right)\cap\left(SCD\right)=MK\) (câu d luôn :v)
\(\Rightarrow MK\cap SC=\left\{P\right\}\Rightarrow P=\left(ABM\right)\cap SC\)