Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

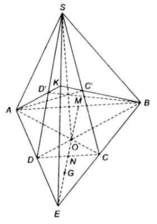
a) Gọi N là giao điểm của EM và CD
Vì M là trung điểm của AB nên N là trung điểm của CD (do ABCD là hình thang)
⇒ EN đi qua G
⇒ S, E, M, G ∈ (α) = (SEM)
Gọi O là giao điểm của AC và BD
Ta có (α) ∩ (SAC) = SO
và (α) ∩ (SBD) = SO = d
b) Ta có: (SAD) ∩ (SBC) = SE
c) Gọi O' = AC' ∩ BD'
Ta có AC' ⊂ (SAC), BD' ⊂ (SBD)
⇒ O' ∈ SO = d = (SAC) ∩ (SBD)

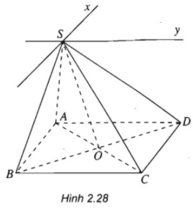
a)
Ta có:
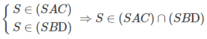
Giả sử:
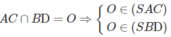
⇒ O ∈ (SAC) ∩ (SBD)
⇒ (SAC) ∩ (SBD) = SO
b) Ta có:
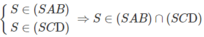
Ta lại có
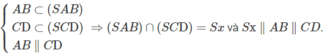
c) Lập luận tương tự câu b) ta có ⇒ (SAD) ∩ (SBC) = Sy và Sy // AD // BC.

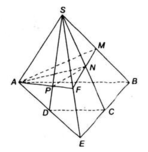
a) Tìm (SAD) ∩ (SBC)
Gọi E= AD ∩ BC. Ta có:
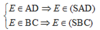
Do đó E ∈ (SAD) ∩ (SBC).
mà S ∈ (SAD) ∩ (SBC).
⇒ SE = (SAD) ∩ (SBC)
b) Tìm SD ∩ (AMN)
+ Tìm giao tuyến của (SAD) và (AMN) :
Trong mp (SBE), gọi F = MN ∩ SE :
F ∈ SE ⊂ (SAD) ⇒ F ∈ (SAD)
F ∈ MN ⊂ (AMN) ⇒ F ∈ (AMN)
⇒ F ∈ (SAD) ∩ (AMN)
⇒ AF = (SAD) ∩ (AMN).
+ Trong mp (SAD), gọi AF ∩ SD = P
⇒ P = SD ∩ (AMN).
c) Tìm thiết diện với mp(AMN):
(AMN) ∩ (SAB) = AM;
(AMN) ∩ (SBC) = MN;
(AMN) ∩ (SCD) = NP
(AMN) ∩ (SAD) = PA.
⇒ Thiết diện cần tìm là tứ giác AMNP.
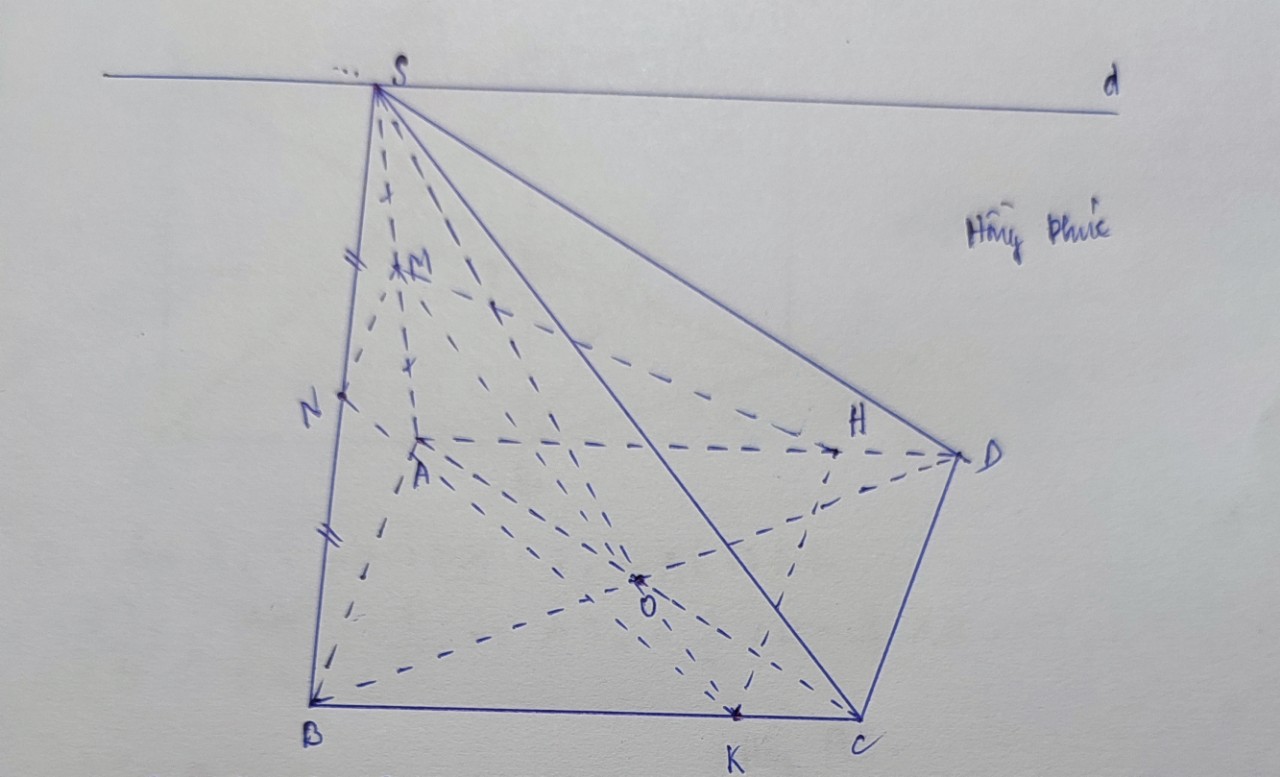
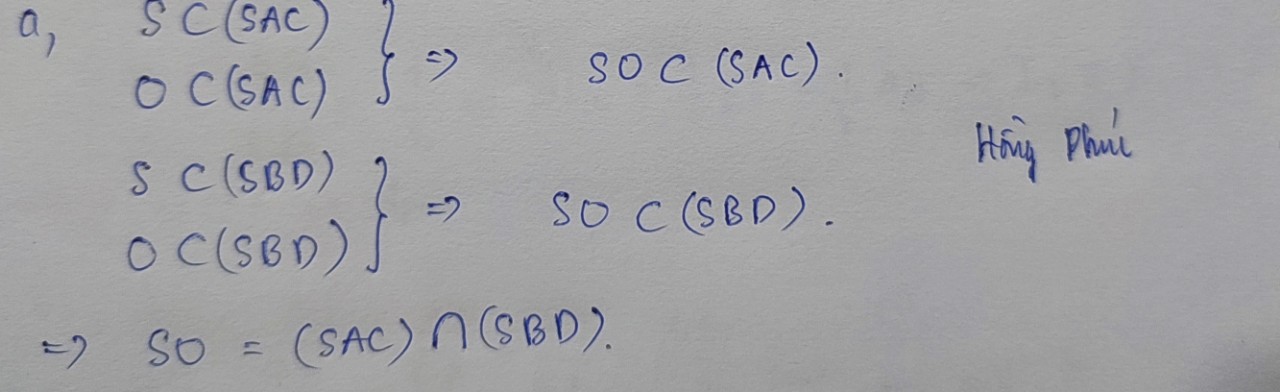
A. (SAC) ∩ (SBD) = SO
B. (SAB) ∩ (SCD) = SE
C. (SAD) ∩ (SBC) = xy
D. nếu S, A, C, D cùng nằm trong một mặt phẳng thì S ∈ (ACD) mâu thuẫn với giả thiết S.ABCD là hình chóp
Đáp án D