Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
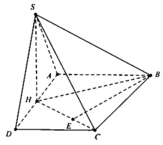
Ta có SAD là tam giác đều nên S H ⊥ A D
Mặt khác S A D ⊥ A B C D ⇒ S H ⊥ A B C D .
Dựng B E ⊥ H C ,
do B E ⊥ S H ⇒ B E ⊥ S H C
Do đó d = B E = 2 a 6 ; S H = a 3 ; A D = 2 a
Do S C = a 15 ⇒ H C = S C 2 − S H 2 = 2 a 3 .
Do S A H B + S C H D = 1 2 a A B + C D = S A B C D 2
suy ra V S . A B C D = 2 V S . H B C = 2 3 . S H . S B C H
= 3 2 a 3 . B E . C H 2 = 4 a 3 6 .

Đáp án B.
Gọi I là trung điểm của SP. Theo định lý Talet:
d 1 H M N = 1 2 d S H M N . Ta cần tính d S H M N .
Bước 1: Tìm V S . H M N
Ta có:
V S . H M N V S . H A D = 1 2 . 1 2 = 1 4 ; V S . H A D V S . A B C D = 1 4
Giả sử a = 1
Dễ thấy
V S . A B C D = 1 3 S H . S A B C D = 1 3 . 3 2 . 3 2 = 1 4
⇒
V
S
.
H
M
N
=
1
16
.
1
4
=
1
64
.
Bước 2: Tìm S H M N . Ta có: M H → = − 1 2 B S → và M N → = 1 2 B C → ⇒ H M N = 180 ° − S B C .
Do đó
sin H M N = sin S B C ⇒ S H M N = 1 2 M H . M N . sin H M N = 1 4 . S S B C .
Tam giác SBC có SB = BC = 1;
S C = S H 2 + H C 2 = 2 S H = 6 2 ⇒ S S B C = 15 8 .
Do đó S H M N = 1 4 . 15 8 = 15 32 .
Bước 3: Sử dụng công thức:
d S H M N = 3. V S . H M N S H M N = 3 64 . 32 15 = 15 10 ⇒ d I H M N = 1 2 . 15 10 = 15 20 .

Chọn đáp án C
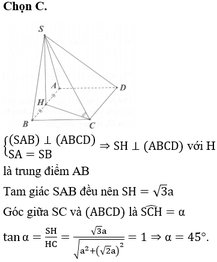
Gọi O là trung điểm AB.
Do tam giác SAB đều và nằm trong mặt phẳng vuông góc (ABCD) nên S O ⊥ A B C D
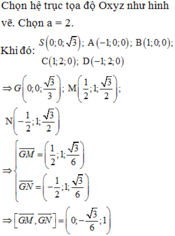
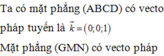

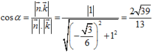

Đáp ánA
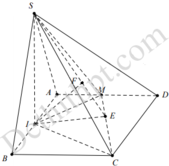
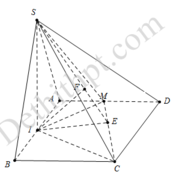
Do Δ S A B đều nên S I ⊥ A B
Mặt khác S A B ⊥ A B C D ⇒ S I ⊥ A B C D
Dựng I E ⊥ C M ; I F ⊥ S E ⇒ d I ; S C M = I F
Ta có: C M = a 5 2 ; S I C M = S A B C D − S I B C − S M C D = S A I M
= a 2 − a 2 4 − a 2 4 − a 2 8 = 3 a 2 8
Do đó I E = 2 S I C M C M = 3 a 5 10 ; S I = a 3 2
Lại có d = I F = S I . I E S I 2 + I E 2 = 3 a 2 8 .
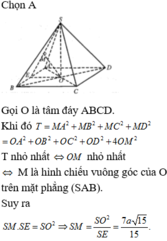
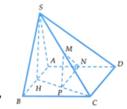



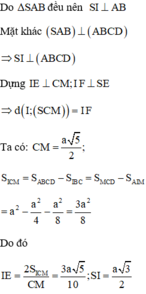
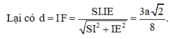
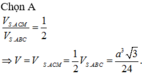
Cho mình hỏi là làm sao để tìm đc MI vậy