

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án D
Dễ thấy rằng:
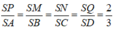
![]()
Giả sử S E ∩ A B = E ' ; S F ∩ C D = F '
Áp dụng định lý Ceva vào tam giác SAB có:

⇔ E ' A = E ' B ⇒ E ' là trung điểm của AB.
Chứng minh tương tự ta cũng có F ' là trung điểm của CD
⇒ E ' F ' là đường trung bình của hình thang ABCD
![]()
Áp dụng định lý Menelaus vào tam giác SBE’ với cát tuyến AEM có:
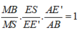
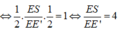
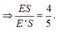
Chứng minh tương tự ta cũng có:
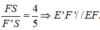
Áp dụng định lý Thales vào tam giác SE’F’ có:
![]()
![]()

Chọn D.
Do ( α ) đi qua G ∈ (SBC), song song với BC nên ( α ) cắt mặt phẳng (SBC) theo giao tuyến MN qua G và song song với BC.
Do tam giác ABC vuông cân tại B, AC = a
2
nên ![]()
Do SA
⊥
(ABC) nên ![]()
![]()