Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
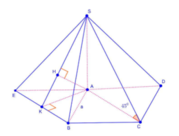
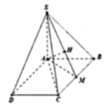
Góc giữa SC và mặt đáy bằng 45 o ⇒ S C A ^ = 45 o
Xét tam giác SAC vuông tại A, ta có
![]()
Dựng hình bình hành ACBE
![]()
Gọi H là hình chiếu của A lên mặt phẳng (SBE).
![]()
![]()
Xét hình tứ diện vuông SABE có
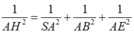
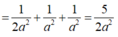
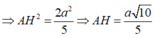

Ta có \(\left(SHC\right)\cap\left(SHD\right)=SH\)
Từ giả thiết \(\left(SHC\right)\perp\left(ABCD\right);\left(SHD\right)\perp\left(ABCD\right)\Rightarrow SH\perp\left(ABCD\right)\)
\(\Leftrightarrow V_{S.ABCD}=\frac{1}{3}SH.S_{ABCD}=\frac{1}{3}AB.AD.SH=\frac{1}{3}a^2\sqrt{3}.SH\left(1\right)\)
Ta có \(SH\perp\left(ABCD\right)\Rightarrow HD\) là hình chiếu của SD trên (ABCD), suy ra góc giữa SD và (ABCD) là \(\widehat{SDH}=60^0\Rightarrow SH=HD\tan\widehat{SDHH}=\frac{a\sqrt{39}}{2}\)
Khi đó \(V_{S.ABCD}=\frac{1}{2}a^3\sqrt{13}\)
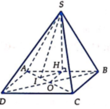
Dựng hình bình hành ACBE. Khi đó AC//BE suy ra AC//(SBE)
\(\Rightarrow d\left(AC,SB\right)=d\left(AC,\left(SBE\right)\right)=d\left(A,\left(SBE\right)\right)=2d\left(H,\left(SBE\right)\right)\)
Gọi K, I lần lượt là hình chiếu của H trên BE và SK.
Khi đó \(BE\perp KH,BE\perp SH\Rightarrow BE\perp HI\left(1\right)\)
Mặt khác \(HI\perp SK\left(2\right)\)
Từ (1) và (2) suy ra \(HI\perp\left(SBE\right)\Rightarrow d\left(H,\left(SBE\right)\right)=HI\)
Tính được \(HK=\frac{a\sqrt{3}}{4};HI=\frac{a\sqrt{39}}{\sqrt{212}}\)
\(\Rightarrow d\left(AC,SB\right)=2d\left(H,\left(SBE\right)\right)=2HI=\frac{a\sqrt{39}}{\sqrt{53}}=\frac{a\sqrt{2067}}{53}\)

Đáp án B
Hướng dẫn giải:
+)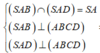
![]()
![]()
+) ![]()
![]()
+) Ta có A B ⊥ B C , kẻ A P ⊥ S B ( P ∈ S B )
d(A;(SBC)) = AP ⇒ d(AD;SB) = AP
+) 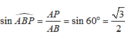
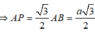
![]()

Đáp án B
Hướng dẫn giải:
Dựng hình bình hành ACDK
![]()
![]()
+Kẻ A P ⊥ D K ⇒ 1 d 2 = 1 S A 2 + 1 A P 2
+ Gọi M = B C ∩ D K
⇒ A C M P l à h i n h c h ữ n h a t
⇒ A P = C M = b 2
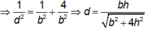
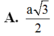
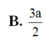
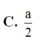
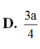

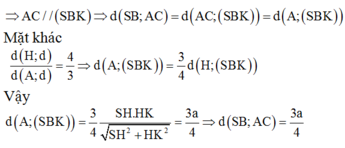

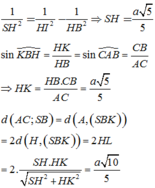
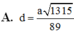
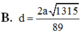
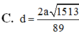
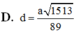

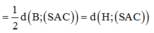

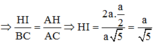
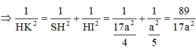
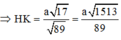
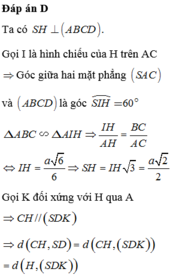

Đáp án: D.
Hướng dẫn giải:
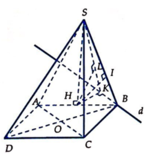
Lấy M là trung điểm BC, H là hình chiếu của A lên SM. Xác định
S A ⊥ B C ⊥ A M
⇒ A H ⊥ S M ⇒ A H ⊥ ( S B C )
⇒ d ( A , ( S B C ) ) = A H
Vì AD//(SBC) chứa BC nên
d(SB,AD)=d(AD,(ABC))=d(A,(SBC))=AH
Tính: SA=AD= a 2 ,AM= a 2
⇒ A H = a 2 5