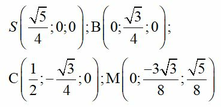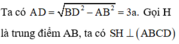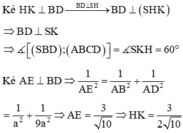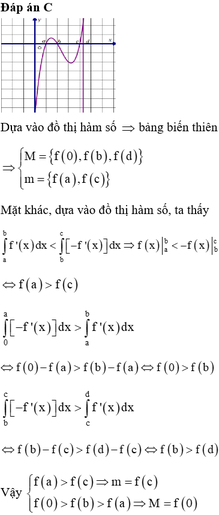Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Gọi H là trung điểm của AD, N là trung điểm của AB
Có S H ⊥ A B C D ⇒ góc giữa SB và A B C D là góc SBH
Có
H B = a 2 + a 2 2 = a 5 2 S H = H B . tan S B H = a 5 2 . tan 60 0 = a 15 2 . S Δ M A B = 1 2 . M N . A B = a 2 2 V S . M A B = 1 3 . S H . S Δ M A B = 1 3 . a 15 2 . a 2 2 = a 3 15 12

Đáp án D
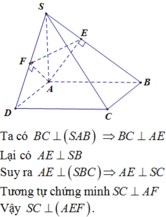
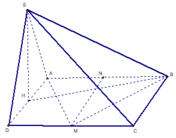
Vì ABCD là hình thang vuông tại A, D
⇒ A D ⊥ C D .
Mà S A ⊥ A B C D ⇒ S A ⊥ S A D ⇒ C D ⊥ S D
⇒ Tam giác SCD vuông tại D
Vì E là trung điểm của AB suy ra AECD là hình vuông
⇒ C E ⊥ A B mà S A ⊥ A B C D ⇒ S A ⊥ A B
suy ra C E ⊥ S A B

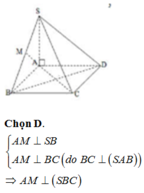
Đáp án A
Phương pháp:
Gọi M là trung điểm của AB, chứng minh S M ⊥ A B C bằng cách sử dụng tính chất của trục đường tròn đáy.
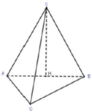
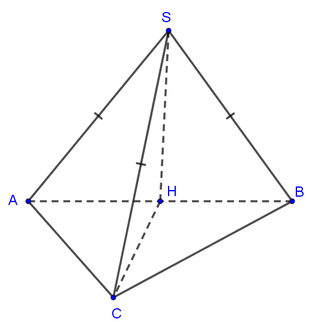
Cách giải: Gọi M là trung điểm của AB.
Vì Δ A B C vuông tại C nên M A = M B = M C . .
Mà S A = S B = S C nên SM là trục đường tròn ngoại tiếp tam giác ABC.
Suy ra S M ⊥ A B C .
Vậy H ≡ M là trung điểm của AB.
Chú ý khi giải: Cần tránh nhầm lẫn với trường hợp chóp tam giác đều: HS dễ nhầm lẫn khi nghĩ rằng S A = S B = S C thì hình chiếu vuông góc của S sẽ là trọng tâm tam giác dẫn đến chọn nhầm đáp án B.

Chọn A
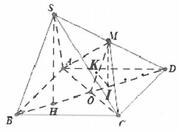
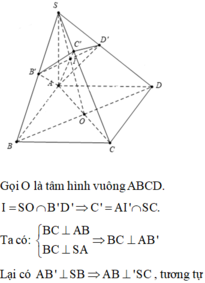
Phương pháp tọa độ (cách này tính toán khá phức tạp nên chỉ nêu ra để học sinh thấy không phải bài toán nào cũng dùng phương pháp tọa độ cũng nhanh nhất)
Ta chọn hệ trục tọa độ như hình vẽ và chọn a = 1.
Ta có: