Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gợi ý xem bạn làm được ko, ko thì để mình trình bày luôn
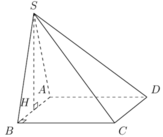
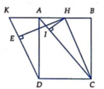
Kẻ \(KC\perp HD;KC\cap HD=\left\{K\right\}\)
\(\left\{{}\begin{matrix}KC\perp HD\\KC\perp SH\end{matrix}\right.\Rightarrow KC\perp\left(SHD\right)\Rightarrow\left(SKC\right)\perp\left(SHD\right)\)
Kẻ \(CI\perp SK;CI\cap SK=\left\{I\right\}\Rightarrow CI\perp\left(SHD\right)\Rightarrow CI\perp\left(SHD\right)\)
\(\Rightarrow\left(SC,\left(SHD\right)\right)=\left(SC,SI\right)\)

Lớp 12 thì chúng ta tọa độ hóa cho đơn giản
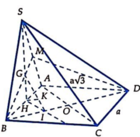
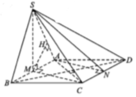
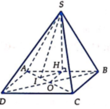
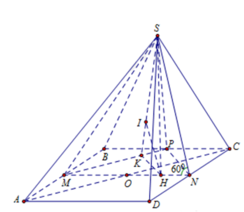
Gọi O là trung điểm AB \(\Rightarrow SO\perp\left(ABCD\right)\)
\(SO=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(AO=BO=\dfrac{a}{2}\)
Đặt hệ trục Oxyz vào chóp, với gốc O trùng O, tia Oz trùng tia OS, tia Ox trùng tia OB, tia Oy trùng tia ON (với N là trung điểm CD). Quy ước \(\dfrac{a}{2}\) là 1 đơn vị độ dài
Ta được tọa độ các điểm: \(S\left(0;0;\sqrt{3}\right)\) ; \(C\left(1;2;0\right)\) ; \(A\left(-1;0;0\right)\) ; \(D\left(-1;2;0\right)\)
Do M là trung điểm SD \(\Rightarrow M\left(-\dfrac{1}{2};1;\dfrac{\sqrt{3}}{2}\right)\)
\(\overrightarrow{AM}=\left(\dfrac{1}{2};1;\dfrac{\sqrt{3}}{2}\right)\) ; \(\overrightarrow{SC}=\left(1;2;-\sqrt{3}\right)\) ; \(\overrightarrow{AC}=\left(2;2;0\right)\)
\(d\left(AM;SC\right)=\dfrac{\left|\left[\overrightarrow{AM};\overrightarrow{SC}\right].\overrightarrow{AC}\right|}{\left|\left[\overrightarrow{AM};\overrightarrow{SC}\right]\right|}=\dfrac{2\sqrt{5}}{5}=\dfrac{a\sqrt{5}}{5}\)
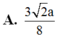
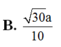
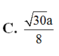
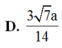

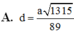
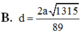
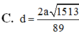
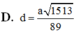

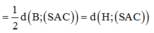

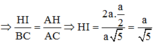
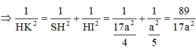
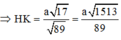


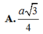
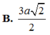
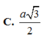
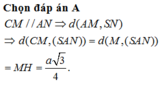

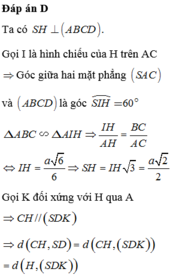

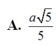
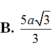
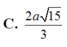
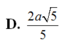
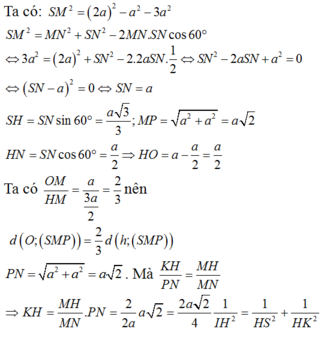
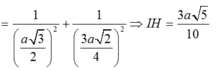
Đáp án A