Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là A
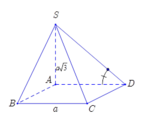
Ta có: S D ; A B C D ^ = S D ; A D ^ = S D A ^ .
Trong tam giác SAD có:
tan S D A ^ = S A A D = a 3 a = 3 ⇒ S D A ^ = 60 0 .

Chọn đáp án A.
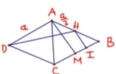
Gọi O là tâm của hình vuông và N là trung điểm của AB.
Khi đó G là giao điểm của AC và DN. Tam giác SGD vuông tại G nên S D G ^ nhọn
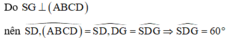


Đáp án B
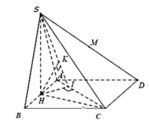
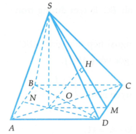
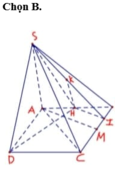
Dễ thấy: S C H ^ = 45 ∘ Gọi H là trung điểm của AB ta có S H ⊥ A B ⇒ S H ⊥ A B C D .
Ta có: S H = H C = a 17 2 .
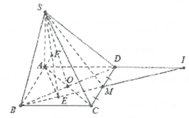
Ta có: d = d M , S A C = 1 2 d D , S A C
Mà 1 2 d D , S A C = 1 2 d B , S A C nên d = d H , S A C
Kẻ H I ⊥ A C , H K ⊥ S I ⇒ d H , S A C = H K
Ta có: H I = A B . A D 2 A C = a 5 5
Từ đó suy ra: d = H K = S H . H I S I = a 1513 89 .




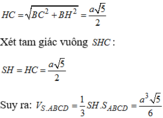
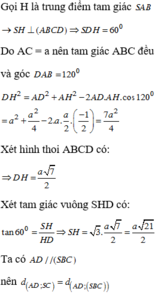

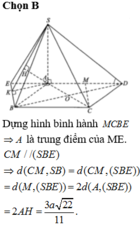
Đáp án A.
Ta có S A ⊥ ( A B C D ) nên A là hình chiếu của S trên mặt phẳng A B C D . Suy ra AD là hình chiếu của SD trên mặt phẳng A B C D .
Khi đó S D , A B C D ^ = S D , A D ^ = S D A ^ (do S D A ^ < 90 ° ).
Do Δ S A D vuông tại A nên tan S D A ^ = S A A D = a 3 a = 3 ⇒ S D A ^ = 60 ° .
Vậy S D , A B C D ^ = 60 ° .