Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
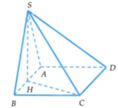
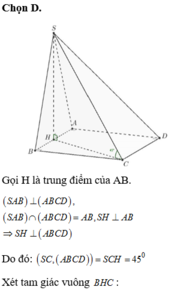
Gọi H là trung điểm của AB. Từ giả thiết ta có S H ⊥ A B C D
Suy ra ![]()
⇒ S H C vuông cân tại H.
Do ∆ B H C vuông tại H nên
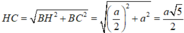
⇒ S H = H C = a 5 2
Thể tích khối chóp V S . A B C D = 1 3 S H . S A B C D = a 3 5 6 đ v t t là

Đáp án D
Phương pháp: Đưa khoảng cách từ M đến (SAC) về khoảng cách từ H đến (SAC).
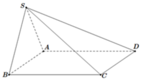
Cách giải: Gọi H là trung điểm của AB ta có SH ⊥ (ABCD)
Ta có (SC;(ABCD)) = (SC;HC) = Góc SCH = 45 0
=>∆SHC vuông cân tại H => 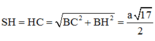
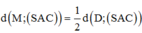
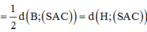
Trong (ABD) kẻ HI ⊥ AC,trong (SHI) kẻ HK ⊥ SI ta có:
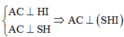
![]()
![]()
Ta có ∆AHI: ∆A CB(g.g) => 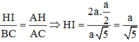
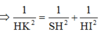
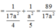
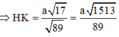

Đáp án B
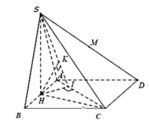
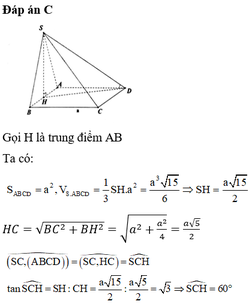
Dễ thấy: S C H ^ = 45 ∘ Gọi H là trung điểm của AB ta có S H ⊥ A B ⇒ S H ⊥ A B C D .
Ta có: S H = H C = a 17 2 .
Ta có: d = d M , S A C = 1 2 d D , S A C
Mà 1 2 d D , S A C = 1 2 d B , S A C nên d = d H , S A C
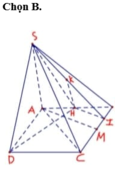
Kẻ H I ⊥ A C , H K ⊥ S I ⇒ d H , S A C = H K
Ta có: H I = A B . A D 2 A C = a 5 5
Từ đó suy ra: d = H K = S H . H I S I = a 1513 89 .

Đáp án B.
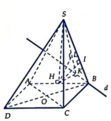
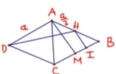
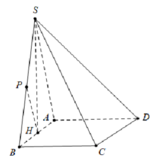
Vẽ đường thẳng d qua B và song song với AC.
Gọi K, I lần lượt là hình chiếu của H trên d và SB, L là hình chiếu của H trên SK.
d ( D , ( S B C ) ) = 2 a 3 ⇔ d A ; ( A B C ) = 2 a 3 ⇔ d H , S B C = a 3 ⇔ H I = a 3
1 S H 2 = 1 H I 2 - 1 H B 2 ⇒ S H = a 5 5
sin K B H ⏞ = H K H B = sin C A B ⏞ = C B A C ⇒ H K = H B . C B A C = a 5 5
d A C ; S B = d A , S B K = 2 d H , S B K = 2 H L = 2 . S H . H K S H 2 + H K 2 = a 10 5

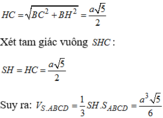
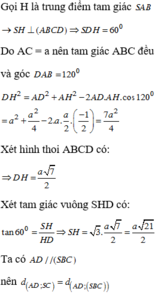


Đáp án D
Phương pháp giải: Dựng hình, xác định khoảng cách giữa hai đường thẳng thông qua mặt phẳng song song với đường thẳng
Lời giải: