Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
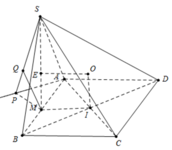
Gọi I và E tương ứng là tâm hình vuông ABCD và tam giác SAB.



Chọn D.
Phương pháp: Xác định cạnh của đáy trước.
Cách giải: Bán kính mặt cầu ngoại tiếp khối chóp là ![]()
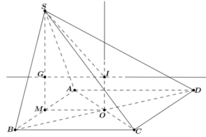
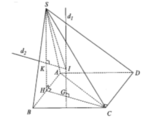
Gọi O là tâm của đáy, I là tâm mặt cầu, G là tâm tam giác SAD, M là trung điểm AD.
Dễ thấy I nằm đồn thời trên trục của tam giác SAD và trục của đáy.
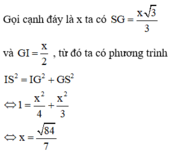
Qua D dựng đường thẳng d song song với AC. Gọi K là hình chiếu cửa M trên d, H là hình chiếu của M trên SD. Suy ra M H ⊥ d , S D .
Ta có:
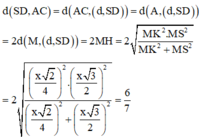

Đáp án B.
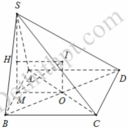
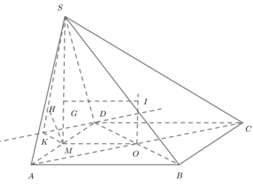
Gọi O là tâm của hính vuông ABCD và H là tâm của đường tròn ngoại tiếp Δ S A B . Từ O kẻ đường thẳng d vuông góc với (ABCD). Từ H kẻ đường thẳng H vuông góc với (SAB).
Ta có d ∩ Δ = I ⇒ I A = I B = I C = IS ⇒ I là tâm đường tròn ngoại tiếp khối chóp S . A B C D ⇒ R = I A = O I 2 + O A 2 .
Mà O I = H M = H B 2 − M B 2 với M là trung điểm của AB.
Xét Δ S A B cân tại S, có A B sin A S B ^ = 2 r
⇒ H B = r = 2 a 2. sin 120 0 = 2 a 3 .
Khi đó O I = 2 a 3 2 − a 2 = a 3 ⇒ R = a 3 2 + a 2 2 = a 21 3 .

Chọn đáp án D
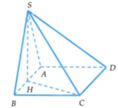
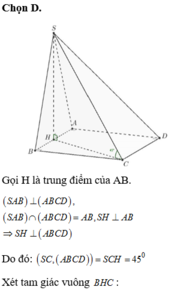
Gọi H là trung điểm của AB. Từ giả thiết ta có S H ⊥ A B C D
Suy ra ![]()
⇒ S H C vuông cân tại H.
Do ∆ B H C vuông tại H nên
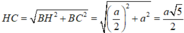
⇒ S H = H C = a 5 2
Thể tích khối chóp V S . A B C D = 1 3 S H . S A B C D = a 3 5 6 đ v t t là


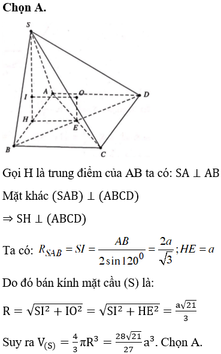



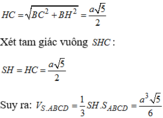
Chọn A.
Phương pháp : Xác định điểm T.