Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/
Ta có
\(CB\perp AB\) (ABCD là hình vuông)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp CB\)
\(\Rightarrow CB\perp\left(SAB\right)\) => CB=a là khoảng cách từ C đến mp (SAB)
b/
Trong mp (SAD) dựng đường thẳng vuông góc với SD cắt SD tại H
Ta có
\(CD\perp AD\) (ABCD là hình vuông)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\)
\(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp AH\)
Mà \(AH\perp SD\)
\(\Rightarrow AH\perp\left(SCD\right)\) => AH là khoảng cách từ A đến mp (SCD)
Xét tg vuông SAD có
\(SD=\sqrt{SA^2+AD^2}=\sqrt{2a^2+a^2}=a\sqrt{3}\) (Pitago)
Ta có
\(AD^2=DH.SD\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow DH=\dfrac{AD^2}{SD}=\dfrac{a^2}{a\sqrt{3}}=\dfrac{a\sqrt{3}}{3}\)
Xét tg vuông ADH có
\(AH=\sqrt{AD^2-DH^2}\) (Pitago)
\(\Rightarrow AH=\sqrt{a^2-\dfrac{a^2}{3}}=\dfrac{a\sqrt{6}}{3}\)
c/ Trong mp (ABCD) Qua O dựng đường thẳng //CD cắt AD tại M và BC tại N => MN//CD (1)
Trong mp (SAD) dựng đường thẳng // AH cắt SD tại Q => MQ // AH
TRong mp (SCD) qua Q dựng đường thẳng //CD cắt SC tại P => QP // CD (2)
Từ (1) và (2) => MN // PQ => M; N; P; Q cùng thuộc 1 mặt phẳng
=> PQ là giao tuyến của mp (MNQP) với mp (SCD)
Trong mp (MNQP) qua O dựng đường thẳng // với MQ cắt QP tại K
Ta có
MQ//AH; OH// MQ => OK//AH
Mà \(AH\perp\left(SCD\right)\)
\(\Rightarrow OK\perp\left(SCD\right)\) => OK là khoảng cách từ O đến mp (SCD)
Xét tứ giác MQKO có
MQ//OK; QP//MN => MQKO là hình bình hành => OK = MQ
Xét tg ACD có
OA=OC (t/c đường chéo hình vuông)
MO//CD
=> MA=MD (trong tg đường thẳng đi qua trung điểm của 1 cạnh // với cạnh thứ 2 thì đi qua trung điểm cạnh còn lai)
Xét tg ADH có
MA=MD (cmt); MQ//AH => QD = QH (trong tg đường thẳng đi qua trung điểm của 1 cạnh // với cạnh thứ 2 thì đi qua trung điểm cạnh còn lai)
=> MQ là đường trung bình của tg ADH
\(\Rightarrow OK=MQ=\dfrac{AH}{2}=\dfrac{1}{2}.\dfrac{a\sqrt{6}}{3}=\dfrac{a\sqrt{6}}{6}\)
d/
Trong mp (SCD) qua H dựng đường thẳng //CD cắt SC tại E => HE//CD
Ta có
AB // CD (Hai cạnh đối hình vuông)
HE // CD
=> AB//HE => A; B; H; E cùng thuộc một mặt phẳng
Trong mp (AHEB) qua e Dựng đường thẳng // AH cắt AB tại I
Ta có
AH//IE; AB//HE => AHEB là hình bình hành => IE=AH
Ta có
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\)
\(AB\perp AD\) (ABCD là hình vuông)
=> \(AB\perp\left(SAD\right)\Rightarrow AB\perp AH\)
Mà AH//IE
\(\Rightarrow AB\perp IE\) (1)
Ta có
\(AH\perp\left(SCD\right)\) (cmt); mà AH//IE \(\Rightarrow IE\perp\left(SCD\right)\Rightarrow IE\perp SC\) (2)
Từ (1) và (2) => IE là khoảng cách giữa AB và SC
\(\Rightarrow IE=AH=\dfrac{a\sqrt{6}}{3}\)

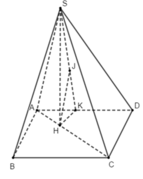
+ Kẻ SH ⊥ AC, H ∈ AC
Do (SAC) ⊥ (ABCD) ⇒ SH ⊥ (ABCD)
+ BD = 2a ⇒ AC = 2a
SA = A C 2 − S C 2 = 2 a 2 − a 3 2 = a ; SH = S A . S C A C = a . a 3 2 a = a 3 2
Ta có: AH = S A 2 − S H 2 = a 2 − a 3 2 2 = a 2 ⇒ AC = 4AH
Lại có: HC ∩ (SAD) = A d C ; S A D d H ; S A D = A C A H = 4
⇒ d(C; (SAD)) = 4d(H; (SAD))
Do BC // (SAD) (BC//AD) ⇒ d(B; (SAD)) = d(C; (SAD))
Do đó d(B; (SAD)) = 4d(H; (SAD))
+ Kẻ HK ⊥ AD tại K, kẻ HJ ⊥ SK tại J
Ta chứng minh được HJ ⊥ (SAD) ⇒ d(H; (SAD)) = HJ
⇒ d(B; (SAD)) = 4HJ
+ Tính HJ
Tam giác AHK vuông tại K có H A K ^ = C A D ^ = 45 ° ⇒ HK = AH.sin 45 ° = a 2 4
Mặt khác: 1 H J 2 = 1 H K 2 + 1 S H 2 ⇒ HJ = a 21 14
Vậy d(B; (SAD)) = 4 . a 21 14 = 2 a 21 7 .
Đáp án C

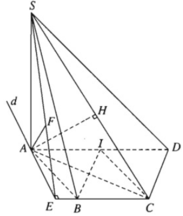
a) Vì ABCD là nửa lục giác đều nội tiếp trong đường tròn đường kính AD = 2a nên ta có: AD //BC và AB = BC = CD = a, đồng thời AC ⊥ CD, AB ⊥ BD, AC = BD = a√3.
Như vậy 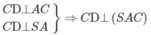
Trong mặt phẳng (SAC) dựng AH ⊥ SC tại H ta có AH ⊥ CD và AH ⊥ SC nên AH ⊥ (SCD)
Vậy AH = d(A,(SCD))
Xét tam giác SAC vuông tại A có AH là đường cao, ta có:
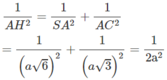
Vậy A H 2 = 2 a 2 ⇒ A H = a 2
Gọi I là trung điểm của AD ta có BI // CD nên BI song song với mặt phẳng (SCD). Từ đó suy ra d(B, (SCD)) = d(I,(SCD)).
Mặt khác AI cắt (SCD) tại D nên
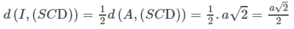
Do đó: 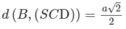
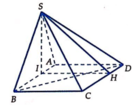
b) Vì AD // BC nên AD // (SBC), do đó d(AD, (SBC)) = d(A,(SBC))
Dựng AD ⊥ BC tại E ⇒ BC ⊥ (SAE)
Dựng AD ⊥ SE tại F ta có:
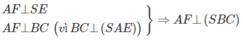
Vậy AF = d(A,(SBC)) = d(AD, (SBC))
Xét tam giác vuông AEB ta có:
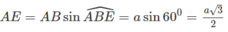
Xét tam giác SAE vuông tại A ta có:
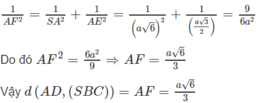

\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}=45^0\Rightarrow AC=SA=a\sqrt{2}\)
\(\Rightarrow AB=a\)
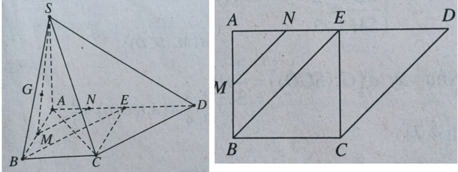
Gọi N là trung điểm SA \(\Rightarrow NM||SB\Rightarrow SB||\left(DMN\right)\)
\(\Rightarrow d\left(DM;SB\right)=d\left(SB;\left(DMN\right)\right)=d\left(B;\left(DMN\right)\right)\)
Mà M là trung điểm AB \(\Rightarrow d\left(B;\left(DMN\right)\right)=d\left(A;\left(DMN\right)\right)\)
Từ A kẻ AH vuông góc DM \(\Rightarrow DM\perp\left(NAH\right)\)
Trong mp (NAH), từ A kẻ \(AK\perp NH\Rightarrow AK=d\left(A;\left(DMN\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AM^2}+\dfrac{1}{AD^2}\Rightarrow AH=\dfrac{AM.AD}{\sqrt{AM^2+AD^2}}=\dfrac{a\sqrt{5}}{5}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AN^2}+\dfrac{1}{AH^2}\Rightarrow AK=\dfrac{AN.AH}{\sqrt{AN^2+AH^2}}=\dfrac{a\sqrt{7}}{7}\)

Đáp án B.
Ta có AD//BC, ![]() => AD//(SBC)
=> AD//(SBC)
=> d(AD;SC) = d(AD;(SBC)) = d(D;(SBC)).
Qua I kẻ đường thẳng song song với AD, cắt CD tại H.
Suy ra IH ⊥ CD
Từ CD ⊥ IH, CD ⊥ SI=> CD ⊥ (SIH)=> CD ⊥ SH
Suy ra ![]()
![]()
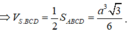
Lại có
![]()
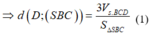
Từ ![]()
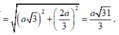
![]()
![]()
Suy ra
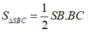
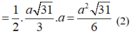
Từ (1) và (2), suy ra
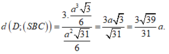
Vậy
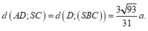

+ Xác định góc của SC với (SAD).
Hạ CE ⊥ AD, ta có E là trung điểm AD và CE ⊥ (SAD) nên ∠(CSE) = 30 o .
∠(CSE) cũng chính là góc giữa SC và mp(SAD).
Trong ΔCSE, ta có:
S E = C E . tan 60 o = a 3 ⇒ S A = S E 2 - A E 2 = 3 a 2 - a 2 = a 2 .
Nhận xét
Gọi M, N lần lượt là trung điểm của AB và AE.
Ta có MN // BE nên MN // CD. Như vậy MN // (SCD). Ta suy ra
d(M,(SCD)) = d(N,(SCD)).
Mà DN/DA = 3/4 nên d(N,(SCD)) = 3/4 d(A,(SCD))
+ Xác định khoảng cách từ A đến (SCD).
Vì vậy tam giác ACD vuông cân tại C nên CD vuông góc với AC.
CD ⊥ AC & CD ⊥ SA ⇒ CD ⊥ (SAC) ⇒ (SCD) ⊥ (SAC).
Hạ AH ⊥ SC, ta có AH ⊥ (SCD).
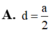
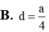
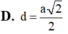
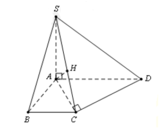

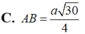
Đáp án C
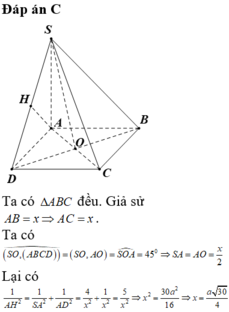
Gọi O = AC ∩ BD Kẻ OK ⊥ SC Do BD ⊥ (SAC) =>BD ⊥ OK
Do đó d(BC;SC) =OK= a 3 2
∆ S A C đ ồ n g d ạ n g ∆ O K C ( g - g )
⇒ S A O K = S C O C ⇔ x a 3 2 = x 2 + 12 a 2 a 3
⇒ x 2 = 6 a 2 ⇒ x = a 6 ⇔ S A = a 6
Khi đó: Kẻ AH ⊥ SD => AH ⊥ (SDC) => AH =d(A;(SCD))
Lại có AB//CD => AB //(SCD) => d(B;(SCD))= d(A;(SCD)=AH
∆ S A D vuông tại A có 1 A H 2 = 1 A S 2 + 1 A D 2 ⇒ A H = a 2