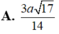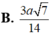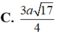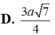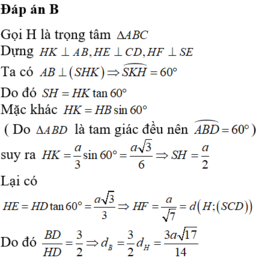Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

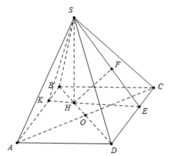
Do tam giác SAB đều và nằm trong mp vuông góc đáy \(\Rightarrow\) H là trung điểm AB
Gọi M là trung điểm AC\(\Rightarrow AM\perp AC\) (trung tuyến đồng thời là đường cao)
Gọi N là trung điểm AM \(\Rightarrow\) NH là đường trung bình tam giác AMH \(\Rightarrow NH||BM\Rightarrow NH\perp AC\)
\(\Rightarrow AC\perp\left(SNH\right)\)
Trong tam giác vuông SNH kẻ \(HK\perp SN\Rightarrow HK=d\left(H;\left(SAC\right)\right)\)
\(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(BM=\dfrac{a\sqrt{3}}{2}\Rightarrow NH=\dfrac{1}{2}BM=\dfrac{a\sqrt{3}}{4}\)
Hệ thức lượng:
\(\dfrac{1}{HK^2}=\dfrac{1}{SH^2}+\dfrac{1}{NH^2}=\dfrac{20}{3a^2}\Rightarrow NH=\dfrac{a\sqrt{15}}{10}\)