K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 6 2021
Chắc là mp (P) đi qua A'
Đặt \(V_{SABCD}=V\)
Theo định lý Talet: \(\dfrac{SA'}{SA}=\dfrac{SB'}{SB}=\dfrac{SC'}{SC}=\dfrac{SD'}{SD}=\dfrac{3}{4}\)
Ta có: \(\dfrac{V_{SA'B'C'D'}}{V_{SABCD}}=\dfrac{2V_{SA'B'C'}}{2V_{SABC}}=\dfrac{V_{SA'B'C'}}{V_{SABC}}=\dfrac{SA'}{SA}.\dfrac{SB'}{SB}.\dfrac{SC'}{SC}=\dfrac{3}{4}.\dfrac{3}{4}.\dfrac{3}{4}=\dfrac{27}{64}\)
Tỉ số thể tích 2 phần (phần trên chia phần dưới) là: \(\dfrac{27}{64}:\left(1-\dfrac{27}{64}\right)=\dfrac{27}{37}\)

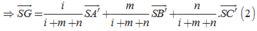

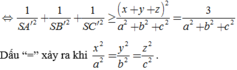
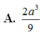
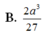


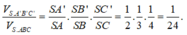

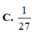
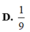
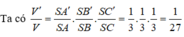

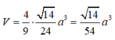

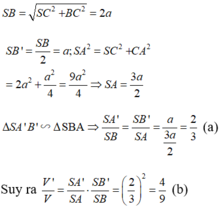


Đáp án A.
Hướng dẫn giải:
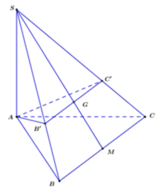
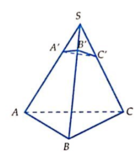
Nếu a = b = c = 1 thì SA = SA',SB = SB',SC = SC'
nên ( A B C ) ≡ ( A ' B ' C ' )
Dễ thấy (A'B'C') đi qua trọng tâm của tam giác ABC
⇒ a + b + c = 3 là đáp án đúng