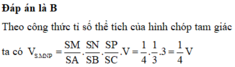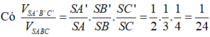Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có
V S . A B C V S M N P = S A S M . S B S N . S C S P = 2 S M S M . 2 S N S N . 1 2 S P S P = 2
⇒ V S M N P = 1 2 V S A B C = V 2

Chọn A.
Phương pháp:
+ Xác định chiều cao của hình chóp bằng cách sử dụng: Nếu SA = SB = SC thì S thuộc trục đường tròn ngoại tiếp tam giác ABC hay chân đường cao hạ từ S xuống (ABC) trùng với tâm đường tròn ngoại tiếp
tam giác . ABC
+ Tính chiều cao SH dựa vào định lý Pyatgo
+ Tính thể tích theo công thức V = 1 3 h . S với h là chiều cao hình chóp, S là diện tích đáy.
Cách giải:
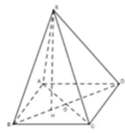


Đáp án A
Ta có
S A ' S A = 2 5 ; S B ' S B = 1 4 ; S C ' S C = 1 3 . ⇒ V S A ' B ' C ' V S A B C = 2 5 . 1 4 . 1 3 = 1 30 .

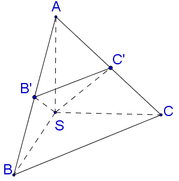
Đáp án C
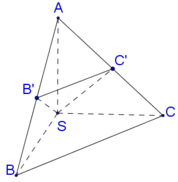
Vì SA=SB=SC suy ra tam giác SAB và tam giác SAC cân tại S. Vậy B′,C′ lần lượt là trung điểm của AB,AC.
Ta có:
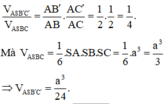

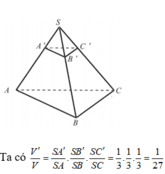
Đáp án D
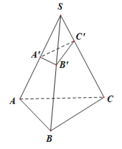
V ' V = V S . A ' B ' C ' V S . A B C = S A ' S A S B ' S B S C ' S C = 1 2 1 3 1 4 = 1 24