Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Cách 1:
Gọi M, N, P lần lượt là trung điểm các cạnh AC, SA, BC.
Khi đó, MN//SC, MP//AB nên góc giữa SC, AB là góc giữa MN và MP, tức N M P ^ hoặc 180 ∘ − N M P ^ .
Có M N = M P = a 2 .
Do S A = S B = S C = A B = A C = a , B C = a 2 nên ΔABC, ΔSBC vuông cân tại A và S
⇒ S P = A P = B C 2 = a 2 2 ⇒ Δ S P A là tam giác vuông cân tại ⇒ P N = S A 2 = a 2 .
Tam giác M N = M P = N P = a 2 ⇒ΔMNP đều ⇒ N M P ^ = 60 ∘ .
Vậy góc giữa hai đường thẳng SC, AB bằng 60 0 .
Cách 2:
Từ giả thiết suy ra ΔSBC vuông cân tại S; ΔSAC là tam giác đều.
Có S C → . A B → = S C → . S B → − S A → = S C → . S B → − S C → . S A → = − S C . S A . c o s A S C ^ = − a . a . cos 60 ∘ = − a 2 2
Có A B = a , S C = a ⇒ cos S C → , A B → = S C → . A B → S C . A B = − a 2 2 a 2 = − 1 2 ⇒ S C → , A B → = 120 ∘ .
Vậy góc giữa hai đường thẳng SC, AB bằng 180 ∘ − 120 ∘ = 60 ∘ .

Chọn đáp án D
Ta có
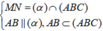
![]()
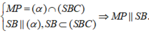
![]()
Khi đó ![]()
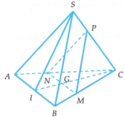
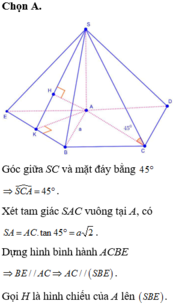
Gọi I là trung điểm của AB.
Ta có SA=SB=AB=CA=CB=a nên tam giác SAB và tam giác ABC đều cạnh a.
Khi đó A B ⊥ S I , A B ⊥ C I và S I = C I = a 3 a
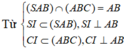
![]()
Mặt khác S I = C I = S C = a 3 2 nên ∆ S I C đều
![]()
Vậy góc giữa hai mặt phẳng (MNP) và (ABC) bằng 60 0

Đáp án B.
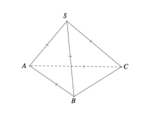
Ta có S B ⊥ ( A B C ) ⇒ B C là hình chiếu của SC trên mặt phẳng (ABC).
Suy ra S C , ( A B C ) ^ = S C , B C ^ = S C B ^ = 60 0
Do Δ A B C vuông tại A nên
S B = B C . tan S C B ^ = 2 a . tan 60 0 = 2 a 3 .
⇒ B C = A B 2 + A C 2 = a 2 + a 3 2 = 2 a .
Do Δ S B C vuông tại B nên
S B = B C . tan S C B ^ = 2 a . tan 60 0 = 2 a 3 .
Vậy
V S . A B C = 1 3 S B . S Δ A B C = 1 6 S B . A B . A C = 1 6 .2. 3 a . a . a 3 = a 3 (đvtt).

Đáp án C
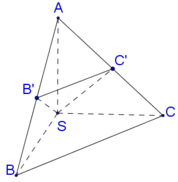
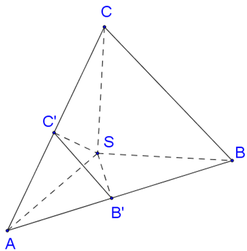
Vì SA=SB=SC suy ra tam giác SAB và tam giác SAC cân tại S. Vậy B′,C′ lần lượt là trung điểm của AB,AC.
Ta có:
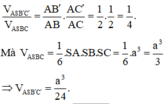

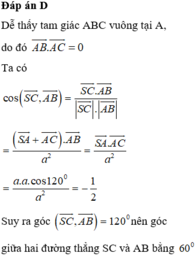

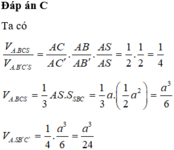

Đáp án là B