Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
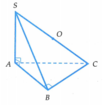
Gọi M là trung điểm của BC. Suy ra M là tâm đường tròn ngoại tiếp tam giác vuông ABC.
Kẻ đường thẳng Δ đi qua M và vuông góc với mặt phẳng (ABC), Δ chính là trục của đường tròn ngoại tiếp đa giác đáy.
Trong mặt phẳng chứa SA và Δ, dựng đường trung trực d của
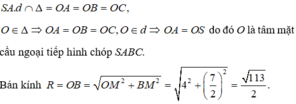

Ta có S A ⊥ A B C A C ⊂ A B C
⇒ S A ⊥ A C
S A ⊥ A B C A B ⊥ B C
⇒ S B ⊥ B C . Tâm I của mặt cầu là trung điểm của cạnh huyền SC.
Bán kính: R = SI = S C 2
S A 2 + A C 2 2 = a 2 + a 2 + a 2 2 = a 3 2
Đáp án D

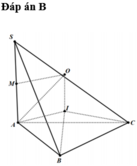
Dựng tam giác đều IAB (I và C cùng phía bờ AB). Ta có ∠ I B C = 120 ° - 60 ° = 60 ° và IB=BC nên DIBC đều, IA=IB=IC=a
Qua I dựng đường thẳng song song với SA, cắt đường trung trực của SA tại O thì O là tâm mặt cầu ngoại tiếp hình chóp.
Gọi M là trung điểm của SA.
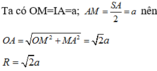

Chọn đáp án C
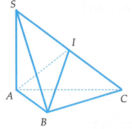
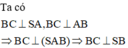
Vậy hai điểm cùng nhìn cạnh dưới một góc vuông. Điều đó chứng tỏ SC là đường kính của mặt cầu ngoại tiếp hình chóp. Do đó bán kính
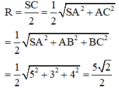

Đáp án C.
Hình chóp S.ABC có đáy ABC là tam giác vuông tại A, cạnh bên SA vuông góc với mặt phẳng (ABC) thì mặt cầu ngoại tiếp hình chóp S.ABC có bán kính r = 1 2 . S A 2 + A B 2 + A C 2 . Với giả thiết của bài toán, ta có r = a 6 2 .
Phân tích phương án nhiễu:
Phương án A: Sai do HS nhớ đúng công thức tính r = 1 2 . S A 2 + A B 2 + A C 2 nhưng lại biến đổi nhầm x 2 + y 2 + z 2 = x + y + z .
Phương án B: Sai do HS có thể gắn hệ trục tọa độ Oxyz vào hình chóp (A trùng với O và B, C, S lần lượt thuộc các tia Ox, Oy, Oz) và nhầm rằng tâm của mặt cầu chính là trọng tâm G a 3 ; a 2 3 ; a 3 3 của tam giác ABC nên tính được r = O G = a 6 3 .
Phương án D: Sai do HS nhớ nhầm công thức r = 1 2 . S A 2 + A B 2 + A C 2 thành r = S A 2 + A B 2 + A C 2 .

Đáp án C
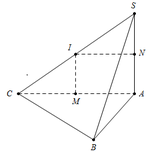
Ta có: Bán kính đường tròn ngoại tiếp tam giác ABC là:
R d = A C 2 = 3 a ⇒ R = S A 2 4 + R 2 d = 5 a .

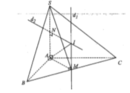


Đáp án D
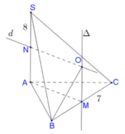
Gọi M là trung điểm của BC. Suy ra M là tâm đường tròn ngoại tiếp tam giác vuông ABC. Kẻ đường thẳng D đi qua M và vuông góc với mặt phẳng (ABC), D chính là trục của đường tròn ngoại tiếp đa giác đáy.
Trong mặt phẳng chứa SA và D, dựng đường trung trực d của SA. d ∩ D = O
do đó O là tâm mặt cầu ngoại tiếp hình chóp SABC