Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác ABC có : \(BC=AB.\tan60^0=2a\sqrt{3}\Rightarrow S_{\Delta ABC}=2a^2\sqrt{3}\)
\(V_{S.ABCD}=\frac{1}{3}SA.S_{\Delta ABC}=\frac{1}{3}a\sqrt{3}.2a^2\sqrt{3}=2a^3\)
- Gọi N là trung điểm cạnh SA. Do SB//(CMN) nên d(SB. CM)=d(SB,(CMN))
=d(B,(CMN))
=d(A,(CMN))
- Kẻ \(AE\perp MC,E\in MC\) và kẻ \(AH\perp NE,H\in NE\), ta chứng minh được \(AH\perp\left(CMN\right)\Rightarrow d\left(A,\left(CMN\right)\right)=AH\)
Tính \(AE=\frac{2S_{\Delta AMC}}{MC}\) trong đó :
\(S_{\Delta AMC}=\frac{1}{2}AM.AC.\sin\widehat{CAM}=\frac{1}{2}a.4a\frac{\sqrt{3}}{2}=a^2\sqrt{3};MC=a\sqrt{13}\)
\(\Rightarrow AE=\frac{2a\sqrt{3}}{\sqrt{13}}\)
Tính được \(AH=\frac{2a\sqrt{3}}{\sqrt{29}}\Rightarrow d\left(A,\left(CMN\right)\right)=\frac{2a\sqrt{3}}{\sqrt{29}}\Rightarrow d\left(SB,CM\right)=\frac{2a\sqrt{3}}{\sqrt{29}}\)

Đáp án B
Hướng dẫn giải:
Dựng hình bình hành ACDK
![]()
![]()
+Kẻ A P ⊥ D K ⇒ 1 d 2 = 1 S A 2 + 1 A P 2
+ Gọi M = B C ∩ D K
⇒ A C M P l à h i n h c h ữ n h a t
⇒ A P = C M = b 2
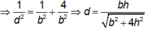
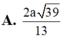
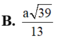
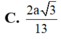
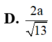
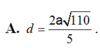
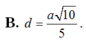
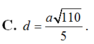
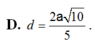


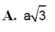
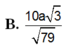
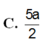
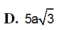
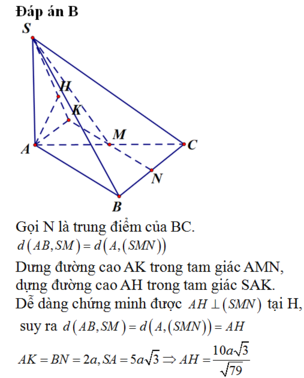

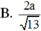

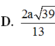

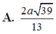
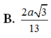
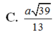
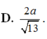


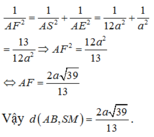
Đáp án: A.
§ Hướng dẫn giải:
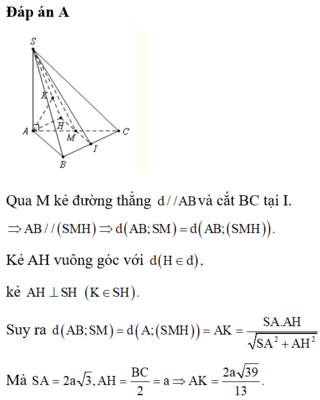
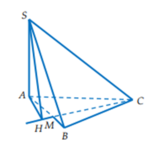
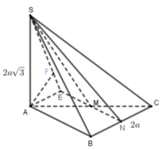
Gọi N là trung điểm của cạnh đáy AC.
Khi đó BC // (SMN)
⇒ d(SM,BC)=d(B,(SMN))=d(A,(SMN))
Gọi H là hình chiếu vuông góc của A trên đoạn SM.
Ta có thể chứng minh được M N ⊥ ( S A M )
từ đó A H ⊥ ( S M N )
Bạn chỉ mình tính AM được không