


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
b: AC vuông góc BD
BD vuông góc SO
=>BD vuông góc (SAC)
=>(SBD) vuông goc (SAC)

a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
SO vuông góc (ABCD)
=>(SBD) vuông góc (ABCD)
b: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
d: (SB;(ABCD))=(BS;BO)=góc SBO
cos SBO=OB/SB=a*căn 2/2/(a*căn 2)=1/2
=>góc SBO=60 độ

Do S.ABCD là chóp tứ giác đều \(\Rightarrow SO\perp\left(ABCD\right)\)
Mà \(O\in AC\Rightarrow SO\in\left(SAC\right)\Rightarrow\left(SAC\right)\perp\left(ABCD\right)\)
Ta có: \(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\Rightarrow SO\perp BD\\AC\perp BD\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Mà \(BD\in\left(SBD\right)\Rightarrow\left(SBD\right)\perp\left(SAC\right)\)

25.
\(\lim\dfrac{3.5^n+7.7^n+9}{6.5^n+9.7^n-3}=\lim\dfrac{7^n\left[3\left(\dfrac{5}{7}\right)^n+7+9.\left(\dfrac{1}{7}\right)^n\right]}{7^n\left[6\left(\dfrac{5}{7}\right)^n+9-3\left(\dfrac{1}{7}\right)^n\right]}\)
\(=\lim\dfrac{3\left(\dfrac{5}{7}\right)^n+7+9\left(\dfrac{1}{7}\right)^n}{6\left(\dfrac{5}{7}\right)^n+9-3\left(\dfrac{1}{7}\right)^n}=\dfrac{3.0+7+9.0}{6.0+9-3.0}=\dfrac{7}{9}\)
26.
\(\lim\left(n-\sqrt{n^2-4n}\right)=\lim\dfrac{\left(n-\sqrt{n^2-4n}\right)\left(n+\sqrt{n^2-4n}\right)}{n+\sqrt{n^2-4n}}\)
\(=\lim\dfrac{4n}{n+\sqrt{n^2-4n}}=\lim\dfrac{4n}{n\left(1+\sqrt{1-\dfrac{4}{n}}\right)}\)
\(=\lim\dfrac{4}{1+\sqrt{1-\dfrac{4}{n}}}=\dfrac{4}{1+\sqrt{1-0}}=2\)
26.
\(u_1=5\)
\(u_n=405=u_1.q^{n-1}\Rightarrow q^{n-1}=\dfrac{405}{5}=81\)
\(\Rightarrow q^n=81q\)
Do \(S_n=\dfrac{u_1\left(1-q^n\right)}{1-q}\Rightarrow605=\dfrac{5\left(1-81q\right)}{1-q}\)
\(\Rightarrow605-605q=5-405q\)
\(\Rightarrow q=3\)

1: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
BD vuông góc CA
BD vuông góc SA
=>BD vuông góc (SAC)
2: DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
=>(SCD) vuông góc (SAD)
4: (SC;(SAB))=(SC;SB)=góc CSB
\(AC=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(SC=\sqrt{AC^2+SA^2}=a\sqrt{5}\)
\(SB=\sqrt{SA^2+AB^2}=2a\)
BC=a
Vì SB^2+BC^2=SC^2
nên ΔSCB vuông tại B
sin CSB=BC/SC=1/căn 5
=>góc CSB=27 độ

1: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
BD vuông góc CA
BD vuông góc SA
=>BD vuông góc (SAC)
2: DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
=>(SCD) vuông góc (SAD)
4: (SC;(SAB))=(SC;SB)=góc CSB
\(AC=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(SC=\sqrt{AC^2+SA^2}=a\sqrt{5}\)
\(SB=\sqrt{SA^2+AB^2}=2a\)
BC=a
Vì SB^2+BC^2=SC^2
nên ΔSCB vuông tại B
sin CSB=BC/SC=1/căn 5
=>góc CSB=27 độ
3: BC vuông góc SAB
=>AE vuông góc BC
mà AE vuông góc SB
nên AE vuông góc (SBC)
=>AE vuông góc SC
4: (SB;(SAC))=(SB;SD)=góc DSB
\(SD=\sqrt{SA^2+AD^2}=2a;SB=2a;DB=a\sqrt{2}\)
\(cosDSB=\dfrac{4a^2+4a^2-2a^2}{2\cdot2a\cdot2a}=\dfrac{3}{4}\)
=>góc DSB=41 độ

\(\left(SAB\right);\left(SAC\right)\) cùng vuông góc (ABCD) \(\Rightarrow SA\perp\left(ABCD\right)\)
\(SA=\sqrt{SD^2-AD^2}=a\sqrt{3}\)
Gọi M là trung điểm CD \(\Rightarrow GS=\dfrac{2}{3}MS\) (t/c trọng tâm)
\(\Rightarrow d\left(G;\left(SBD\right)\right)=\dfrac{2}{3}d\left(M;\left(SBD\right)\right)\)
Gọi I là giao điểm AM và BD \(\Rightarrow\dfrac{IM}{IA}=\dfrac{DM}{AB}=\dfrac{1}{2}\)
\(\Rightarrow d\left(M;\left(SBD\right)\right)=\dfrac{1}{2}d\left(A;\left(SBD\right)\right)\Rightarrow d\left(G;\left(SBD\right)\right)=\dfrac{1}{3}d\left(A;\left(SBD\right)\right)\)
Kẻ AH vuông góc SO (O là tâm đáy) \(\Rightarrow AH\perp\left(SBD\right)\Rightarrow AH=d\left(A;\left(SBD\right)\right)\)
\(AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\) ; \(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AO^2}\Rightarrow AH=\dfrac{SA.AO}{\sqrt{SA^2+AO^2}}=\dfrac{a\sqrt{21}}{7}\)
\(\Rightarrow d\left(G;\left(SBD\right)\right)=\dfrac{1}{3}AH=\dfrac{a\sqrt{21}}{21}\)

a) Theo giả thiết, S.ABCD là hình chóp đều và đáy ABCD là hình vuông nên SO ⊥ (ABCD) ( tính chất hình chóp đều)
Đáy ABCD là hình vuông cạnh a nên
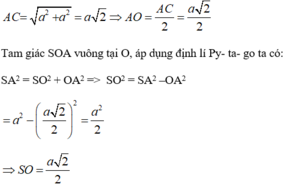

=> Góc giữa hai mặt phẳng (MBD) và (ABCD) là 45 o