Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

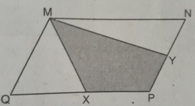
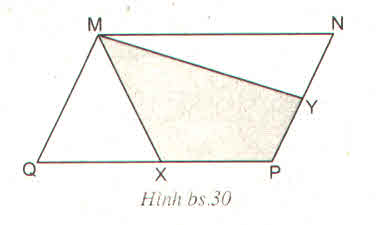
Kẻ đường chéo MP
Ta được SMQX= SMPX
SMNY=SMPY
=> SMXPY= SMPX + SMPY
Khi đó \(S_{MXPY}=\dfrac{1}{2}S\)
Nhớ tick nhé !
Sau khi kẻ đường thẳng MP ta có:
\(\Delta MPQ=\Delta MPN\) (cạnh-cạnh-cạnh)
=> \(\dfrac{1}{2}\)SMPQ = \(\dfrac{1}{2}S_{MPN}\)
hay \(\Delta MPX=\Delta MPY\).
Vì \(S_{MPX}+S_{MPY}=S_{MXPY}=S_{MXQ}+S_{MYN}\) nên SMXPY = \(\dfrac{1}{2}S\).
Vậy SMXPY = \(\dfrac{1}{2}S\).

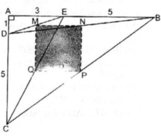
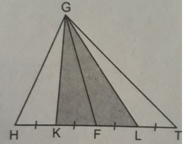
△ DMC có CM = 2/3BC
Hình bình hành ABCD và ΔDMC có chung đường cao kẻ từ đỉnh D đến BC.
Gọi độ dài đường cao là h, BC = a
Ta có diện tích hình bình hành ABCD là S = a h
S D M C = 1/2 h. 2/3 a = 1/3 ah = 1/3 S
S A B M D = S A B C D - S D M C = s - 1/3 S = 2/3 S

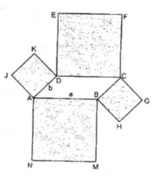
Hình đa giác đó gồm hình bình hành ABCD, hình vuông ABMN, BHGC, CFED, DKJA.
S A B M N = S C D E F = a 2
S B H G C = S D K J A = b 2
Diện tích đa giác bằng :
S A B M N = S C D E F = a 2
S B H G C = S D K J A = b 2

Gọi I là trung điểm của AD, K là giao điểm của CI và BD. Kẻ ME ^ BD tại E, CF ^ BD tại F.
Có B N = 1 3 B D , E M = 1 2 C F S B M N = 1 2 E M . B N = 1 2 . 1 2 C F . 1 3 B D = 1 6 S B C D = 1 12 S ⇒ S M N D C = 1 2 S − 1 12 S = 5 12 S
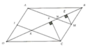

Giải: Xét tam giác ACD có F,G lần lượt là trung điểm AC,DC nên FG là đường trung bình
⇒⇒FG//ADFG//AD
C/m tương tự đc EH//AD;GH//EF//BCEH//AD;GH//EF//BC
⇒EFGH⇒EFGH là hình bình hành
a/Để EFGH là hình chữ nhật thì góc FGH=90oFGH=90o
⇒gócHGD+gócFGC=90o⇒gócHGD+gócFGC=90o
Mà góc HGD=góc BCD;góc FGC= góc ADC ( góc đồng vị = nhau)
⇒⇒ góc BCD+góc ADC=90o90o
⇒⇒Để EFGH là hình chữ nhật thì tứ giác ABCD cần có góc BCD+góc ADC=90o90o
b/Để EFGH là hình thoi thì FG=HG
Mà FG=1/2AD; HG=1/2BC
⇒⇒AD=BC
⇒⇒Để EFGH là hình thoi thì tứ giác ABCD có AD=BC
c/ để EFGH là hình vuông thì EFGH phải vừa là hình chữ nhật vừa là hình thoi⇒⇒ABCD phải có đủ cả hai điều kiện trên
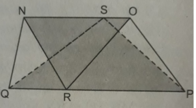
Nối A với C ta có AP là đường trung tuyến của ΔACDΔACD nên
SADP=SAPC=12SADC=14SABCDSADP=SAPC=12SADC=14SABCD
Tương tự SACR=SBCR=12SABC=14SABCD.SACR=SBCR=12SABC=14SABCD.
⇒SAPC+SACR=SARCP=12SABCD.⇒SAPC+SACR=SARCP=12SABCD.
SADP=SAPC=12SADC=14SABCDSADP=SAPC=12SADC=14SABCD
Tương tự SACR=SBCR=12SABC=14SABCD.SACR=SBCR=12SABC=14SABCD.
⇒SAPC+SACR=SARCP=12SABCD.⇒SAPC+SACR=SARCP=12SABCD.
Gọi H là giao điểm của AP và BQ, K là giao điểm của CR và BQ, M là giao điểm của AP và DS, N là giao điểm của CR và DS.
Dễ thấy HKNM là hình bình hành nên các tam giác sau đây có cùng diện tích:
SAKH=SHKM=SMNH=SMNCSAKH=SHKM=SMNH=SMNC=SAKB=SMCD=SAKB=SMCD
Mà SAKR=12SAKBSAKR=12SAKB (đáy gấp đôi, chung đường cao)
Tương tự SMPC=12SMCDSMPC=12SMCD
⇒SAKH=SHKM=SMNH⇒SAKH=SHKM=SMNH=SMNC=(SAKR+SMPC)=SMNC=(SAKR+SMPC)=15SARCP.=15SARCP.
Mà SARCP=12SABCDSARCP=12SABCD
⇒SHKM+SMKN=15SABCD⇒SHKM+SMKN=15SABCD hay SKHMN=15SABCD.
Chọn B