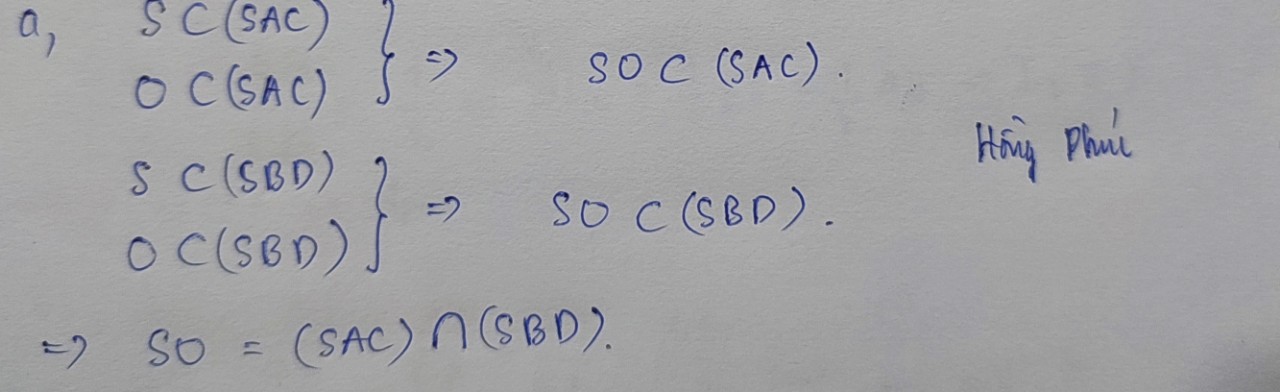Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

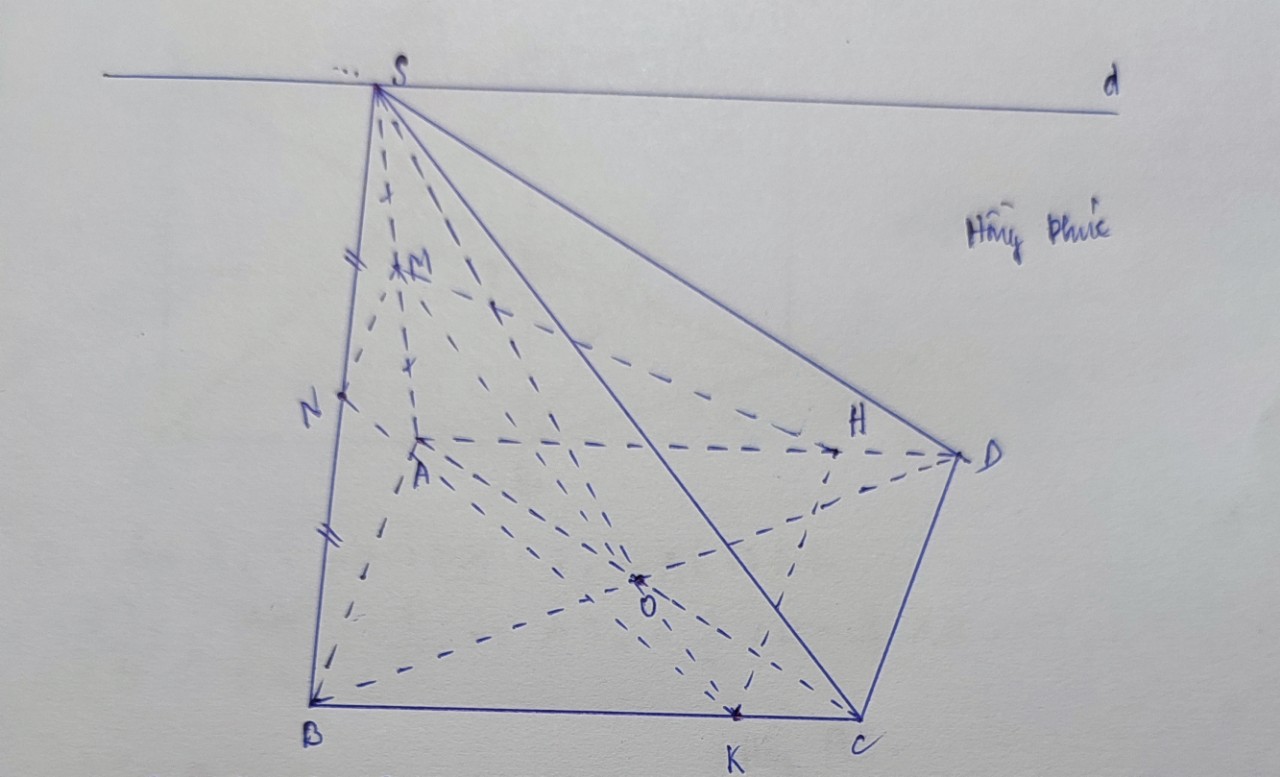
a) Tìm thiết diện :
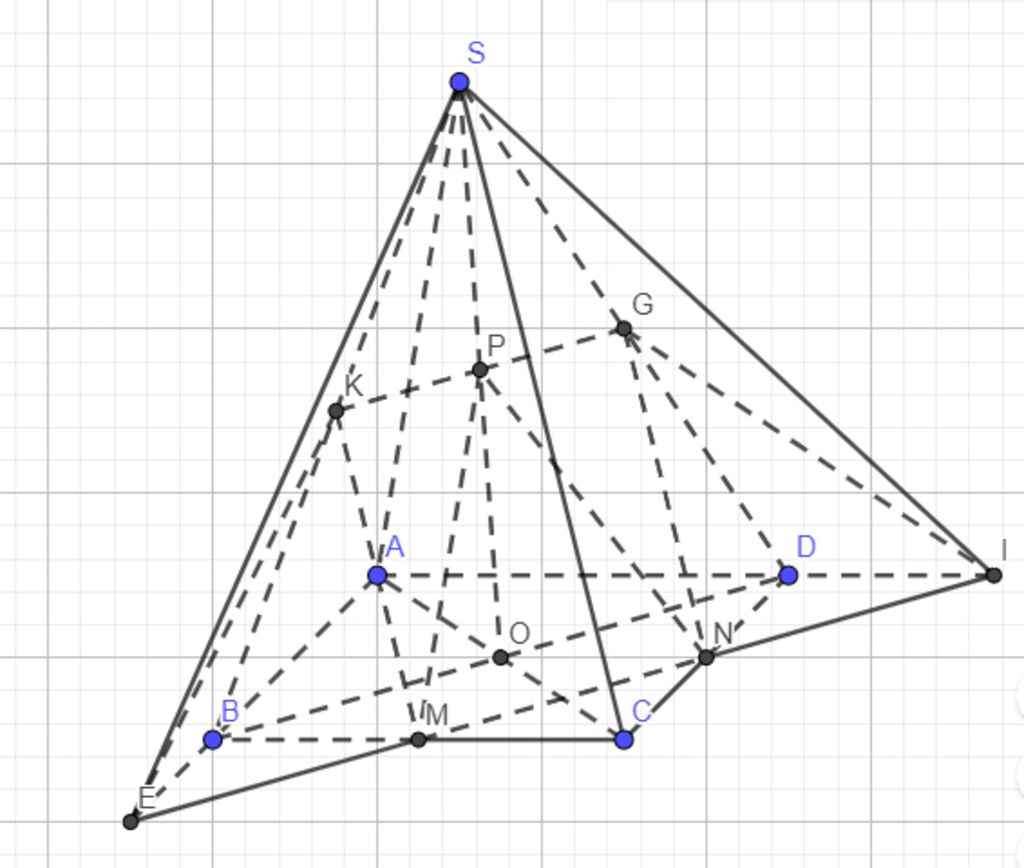
Trong mp(ABCD), gọi F = AD ∩ PN và E = AB ∩ PN
Trong mp(SAD), gọi Q = MF ∩ SD
Trong mp(SAB), gọi R = ME ∩ SB
Nối PQ, NR ta được các đoạn giao tuyến của mp(MNP) với các mặt bên và mặt đáy của hình chóp là MQ, QP, PN, NR, RM
Vậy thiết diện cắt bởi mặt phẳng (MNP) là ngũ giác MQPNR.
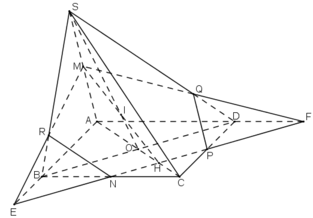
b) Tìm SO ∩ (MNP). Gọi H là giao điểm của AC và PN .
Trong (SAC), SO ∩ MH = I
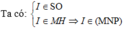
Vậy I = SO ∩ (MNP).

a, Gọi \(I=AC\cap BD\)
Mà \(AC\in\left(SAC\right);BD\in\left(SBD\right)\)
\(\Rightarrow I=\left(SAC\right)\cap\left(SBD\right)\)
Lại có \(S=\left(SAC\right)\cap\left(SBD\right)\Rightarrow SI\) là giao tuyến cần tìm.
b, Gọi \(K=AC\cap BM\)
Mà \(AC\in\left(SAC\right);BM\in\left(SBM\right)\)
\(\Rightarrow K=\left(SAC\right)\cap\left(SBM\right)\)
Lại có \(S=\left(SAC\right)\cap\left(SBM\right)\Rightarrow SK\) là giao tuyến cần tìm.
c, Gọi \(N=AD\cap BM\)
Mà \(AD\in\left(SAD\right);BM\in\left(SBM\right)\)
\(\Rightarrow N=\left(SAD\right)\cap\left(SBM\right)\)
Lại có \(S=\left(SAD\right)\cap\left(SBM\right)\Rightarrow SN\) là giao tuyến cần tìm.
d, Gọi \(T=AM\cap BC\)
Mà \(AM\in\left(SAM\right);BC\in\left(BMC\right)\)
\(\Rightarrow T=\left(SAM\right)\cap\left(SBC\right)\)
Lại có \(S=\left(SAM\right)\cap\left(SBC\right)\Rightarrow ST\) là giao tuyến cần tìm.