Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: ED là đường trung bình của ΔABC
Suy ra: ED//BF và ED=BF
hay BEDF là hình bình hành

a: Xét tứ giác MHKQ có
MH//QK
MH=QK
Do đó: MHKQ là hình bình hành
mà MH=MQ
nên MHKQ là hình thoi

a) Do AM = DN Þ MADN là hình bình hành
⇒ D ^ = A M N ^ = E M B ^ = M B C ^
Ta có DMPE = DBPE nên EP = FP. Vậy MEBF là hình thoi và 2 điểm E, F đối xứng nhau qua AB.
b) Tứ giác MEBF có MB Ç EF = P; Lại có P trung điểm BM, P là trung điểm EF, MB ^ EF.
Þ MEBF là hình thoi.
c) Để BNCE là hình thang cân thì C N E ^ = B E N ^
Mà
C N E ^ = D ^ = M B C ^ = E B M ^ nên DMEB có 3 góc bằng nhau, suy ra điều kiện để BNCE là hình thang cân thì A B C ^ = 60 0
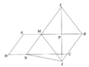

a. Ta có:
\(\left\{{}\begin{matrix}ME=\dfrac{1}{2}MN\\FQ=\dfrac{1}{2}PQ\\MN=PQ\end{matrix}\right.\) \(\Rightarrow ME=FQ\)
Mặt khác: \(MN//PQ\Rightarrow ME//FQ\)
Tức giác MEFQ có một cặp cạnh đối ME,FQ song song và bằng nhau. Do đó từ giác MEFQ là hình bình hành.
b.Xét tứ giác QENF ta có:
\(EN=\dfrac{1}{2}MN=\dfrac{1}{2}PQ=FQ\)
\(MN//PQ\Rightarrow EN//FQ\)
Tứ giác QENF có cặp cạnh đối EN, FQ song song và bằng nhau nên từ giác QENF là hình bình hành. Suy ra QE = NF.