Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

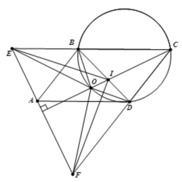
1). Tứ giác OBCD nội tiếp và CO là phân giác góc B C D ^ , suy ra O B D ^ = O C D ^ = O C B ^ = O D B ^ , nên tam giác OBD cân tại O, do đó OB=OD (1).
Tứ giác OBCD nội tiếp O D C ^ = O B E ^ (cùng bù với góc OBC) (2).
Trong tam giác CEF có CO vừa là đường cao vừa là đường phân giác nên tam giác CEF cân tại ![]() .
.
Do A B ∥ C F ⇒ A E B ^ = A F C ^ = E A B ^ , suy ra tam giác ABE cân tại B, nên B E = B A = C D ( 3 )

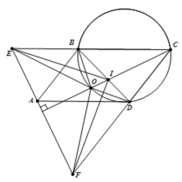
![]() .
.
3). Theo trên, ta có B E = C D mà C E = C F ⇒ B C = D F .
Ta có CI là đường phân giác góc BCD, nên I B I D = C B C D = D F B E ⇒ I B . B E = I D . D F .
Mà CO là trung trực EF và I ∈ C O , suy ra IE=IF.
Từ hai đẳng thức trên, suy ra I B . B E . E I = I D . D F . F I .

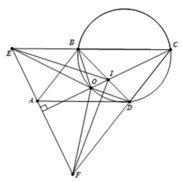
2). Từ Δ O B E = Δ O D C ⇒ O E = O C .
Mà CO là đường cao tam giác cân CEF , suy ra OE=OF.
Từ đó
O
E
=
O
C
=
O
F
, vậy O là tâm đường tròn ngoại tiếp tam giác ![]() .
.

Từ giả thiết suy ra khoảng cách giữa 2 đường thẳng song song AB, CD bằng 4.
Từ đó, do A, B thuộc Ox nên C(c;4), D(d;4)
Vì 2 đường chéo AC, BD cắt nhau tại I nằm trên đường thẳng y=x nên ta có hệ :
\(\begin{cases}2x=c+1=d+2\\2x=0+4\end{cases}\)
Từ đó tìm được x=2, c=3, d=2.
Vậy C(3;4), D(2;4)
cho mình hỏi hình bình hành có diện tích bằng 4 thì sao suy ra được khoảng cách giữa 2 đường thẳng song song =4

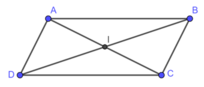
Ta có: A là giao điểm của AB và AD. Do đó, tọa độ A là nghiệm của hệ phương trình:
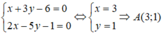
Hình bình hành ABCD có tâm I nên I là trung điểm của AC và BD ⇒ C(-1;3)
Đường thẳng BC đi qua C và song song với AD
Vì BC song song với AD nên BC có dạng: 2x - 5y + c = 0, (c ≠ -1)
Vì C thuộc BC nên: 2.(-1) - 5.3 + c = 0 ⇒ c = 17(tm)
Vậy phương trình đường thẳng BC là: 2x - 5y + 17 = 0
Đường thẳng DC đi qua C và song song với AB
Vì DC song song với AB nên DC có dạng: x + 3y + c = 0, (c ≠ -6)
Vì C thuộc DC nên: -1 + 3.3 + c = 0 ⇒ c = -8(tm)
Vậy phương trình đường thẳng DC là: x + 3y - 8 = 0

Chọn B
Vì ABCD là hình bình hành nên AB//CD
do đó AB đi qua A và nhận vtpt của CD là (3; -4) làm vtpt.
Suy ra đường thẳng AB có vtcp (-4; -3) nên phương trình tham số của đường thẳng AB là
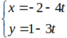

Thay tọa độ A vào 2 pt đường thẳng không thỏa mãn, vậy đó là 2 pt đường thẳng của các cạnh BC và CD
\(\Rightarrow\) Khoảng cách từ A đến 2 đường thẳng nói trên bằng độ dài 2 cạnh của hcn
\(\Rightarrow S=d\left(A;\Delta_1\right).d\left(A;\Delta_2\right)=\dfrac{\left|3-2.\left(-1\right)+1\right|}{\sqrt{1^2+\left(-2\right)^2}}.\dfrac{\left|2.3-1\right|}{\sqrt{2^2+1^2}}=6\)

Bài này bạn chia làm 2 trường hợp Q thuộc đoạn AD và Q nằm ngoài AD
- Trường hợp 1
Từ gt => OA=5, OQ=4, và OM=ON=OP=3
Áp dụng định lý Pytago cho các tam giác QAO và tam giác MAO vuông ứng ứng lần lượt tại Q và M ta có:
AQ2=AO2-OQ2=52-42=32 => AQ+3
AM2=AO2-OM2=52-32=42 => AM=4
=> AM=QO và AQ=MO => AMOQ là hình bình hành
Mà \(\widehat{AMO}=90^o\) => AMOQ là hình chữ nhật
=> \(\widehat{QAM}=90^o\)
Từ đó ta có ABCD là hình chữ nhật
Đặt CP=CN=x
Áp dụng định lý Pytago cho tam giác ABC vuông tại B, với BM=ON=3
AP=AM=4; AB=AM+BM=7
ta có: CA2=AB2+BC2 <=> (x+4)2=72+(x+3)2
=> x=21 và BC=24
Vậy diện tích hình bình hành ABCD là 7.24=168 (đv diện tích)
- Trường hợp 2: Q nằm ngoài đoạn AD
Cmtt trường hợp 1 ta tính được
\(\widehat{ACB}=90^o;AC=7;BC=24\)
Từ đó ta tính được
SABCD=168 (đv diện tích)
 Trong mặt phẳng Oxy, cho hình vuông ABCD có đình M(-–-3;5), tâm I thuộc đường thẳng d : y =−x+5 và diện tích của hình vuông ABCD bằng 25 . Tim tọa độ các đỉnh của hình vuông ABCD, biết rằng tâm I có hoành độ dương
Trong mặt phẳng Oxy, cho hình vuông ABCD có đình M(-–-3;5), tâm I thuộc đường thẳng d : y =−x+5 và diện tích của hình vuông ABCD bằng 25 . Tim tọa độ các đỉnh của hình vuông ABCD, biết rằng tâm I có hoành độ dương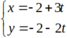
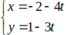
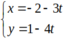
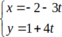
Gọi K, H, I, J lần lượt là trung điểm của ON,OQ,OM,OP
Xét 25 đường thẳng đã cho, với mỗi đường thẳng đó, có một trong hai trường hợp sau :
+) Đường thẳng cắt cạnh AB,CD. Khi đó nó đi qua K hoặc H
+) Đường thẳng cắt cạnh AD,BC. Khi đó nó đi qua I hoặc J
Vậy, có 7 đường thẳng cùng đi qua một trong 4 điểm I,J,K,H( điều phải chứng minh)