Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Ta có A E D ^ = E D C ^ v à A B F ^ = E D C ^ ⇒ D E / / B F (có góc ở vị trí đồng vị bằng nhau).
b) Từ câu a) suy ra DEBF là hình bình hành.
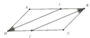
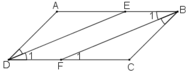
a) Ta có:
+ ABCD là hình bình hành ⇒ AB // CD ⇒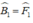 
(Hai góc đồng vị) (1)
+ DE là tia phân giác của góc D
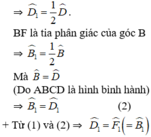
Mà hai góc này ở vị trí đồng vị ⇒ DE // BF (đpcm)
b) Tứ giác DEBF có:
DE // BF (chứng minh ở câu a)
BE // DF (vì AB // CD)
⇒ DEBF là hình bình hành.
a: Ta có: \(\widehat{ADE}=\dfrac{\widehat{ADC}}{2}\)
\(\widehat{CBF}=\dfrac{\widehat{CBA}}{2}\)
mà \(\widehat{ADC}=\widehat{CBA}\)
nên \(\widehat{ADE}=\widehat{CBF}\)
Xét ΔADE và ΔCBF có
\(\widehat{ADE}=\widehat{CBF}\)
AD=BC
\(\widehat{DAE}=\widehat{BCF}\)
Do đó: ΔADE=ΔCBF
Suy ra: AE=CF
Ta có: AE+EB=AB
CF+DF=CD
mà AB=CD
và AE=CF
nên EB=DF
Xét tứ giác DEBF có
EB//DF
EB=DF
Do đó: DEBF là hình bình hành
Suy ra: DE//BF
d: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
e: Ta có: ABCD là hình bình hành
nên Hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường\(\left(1\right)\)
Ta có: EBFD là hình bình hành
nên Hai đường chéo EF và BD cắt nhau tại trung điểm của mỗi đường\(\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra AC,BD,EF đồng quy
Xét ΔADE và ΔCBF có
\(\widehat{ADE}=\widehat{CBF}\)
AD=CB
\(\widehat{A}=\widehat{C}\)
Do đó: ΔADE=ΔCBF
Suy ra: AE=CF và DE=BF
Ta có: AE+BE+AB
CF+FD=CD
mà AB=CD
và AE=CF
nên BE=FD
Xét tứ giác BEDF có
BE=DF
DE=BF
Do đó: BEDF là hình bình hành
Suy ra: DE//BF