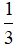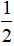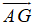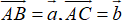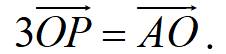Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a.
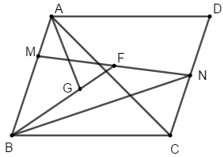
$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$ (tính chất hình bình hành)
b.
$\overrightarrow{AM}=\frac{2}{3}\overrightarrow{AC}=\frac{2}{3}(\overrightarrow{AB}+\overrightarrow{AD})$
c.
$\overrightarrow{AN}=\overrightarrow{AC}+\overrightarrow{CN}=\overrightarrow{AC}+\frac{1}{2}\overrightarrow{BA}$
$=\overrightarrow{AB}+\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}$
$=\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}$

HD: \(\overrightarrow{BC}=\frac{-2}{3}\overrightarrow{AM}+\frac{4}{3}\overrightarrow{AN};\overrightarrow{CD}=\frac{-4}{3}\overrightarrow{AM}+\frac{2}{3}\overrightarrow{AN}\)

\(3\overrightarrow{AP}-2\overrightarrow{AC}=\overrightarrow{0}\)
\(VT=3\left(\overrightarrow{AD}+\overrightarrow{DP}\right)-2\left(\overrightarrow{AD}+\overrightarrow{DC}\right)\)
\(=3\overrightarrow{AD}+3\overrightarrow{DP}-2\overrightarrow{AD}-2\overrightarrow{DC}\)
\(=\overrightarrow{AD}+3\overrightarrow{DP}-2\overrightarrow{DC}\)
\(=\overrightarrow{AD}+3\left(\overrightarrow{DC}+\overrightarrow{CP}\right)-2\overrightarrow{DC}\)
\(=\overrightarrow{AD}+3\overrightarrow{DC}+3\overrightarrow{CP}-2\overrightarrow{DC}\)
\(=\widehat{AD}+\overrightarrow{DC}+3.\dfrac{2}{3}\overrightarrow{CO}\)
\(=\overrightarrow{AD}+\overrightarrow{DC}+2.\dfrac{1}{2}\overrightarrow{CA}\)
\(=\overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{CA}\)
\(=\overrightarrow{AC}+\overrightarrow{CA}\)
\(=\overrightarrow{AA}=\overrightarrow{0}=VP\) (điều phải chứng minh)

a) N trung điểm AD \(\Rightarrow AN=\frac{AD}{2}=\frac{BC}{2}\)
M trung điểm BC \(\Rightarrow MC=\frac{BC}{2}\Rightarrow AN=MC\)mà AN//MC
nên AMCN là hình bình hành \(\Rightarrow\overrightarrow{AM}=\overrightarrow{NC}\)
b) Tương tự câu a ta được \(\hept{\begin{cases}ND=BM=\frac{1}{2}BC\\ND//BM\end{cases}}\)=> NDMB là hình bình hành=> NB//DM (1)
Xét 2 tam giác ANI và NDK: \(\hept{\begin{cases}AN=ND=\frac{AD}{2}\\\widehat{NAI}=\widehat{DNK}\left(AM//NC\right)\\\widehat{ANI}=\widehat{NDK}\left(NB//MD\right)\end{cases}\Rightarrow\Delta ANI=\Delta NDK\left(g.c.g\right)}\)
\(\Rightarrow NI=DK\)(2)
(1), (2) => \(\overrightarrow{NI}=\overrightarrow{DK}\)