Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

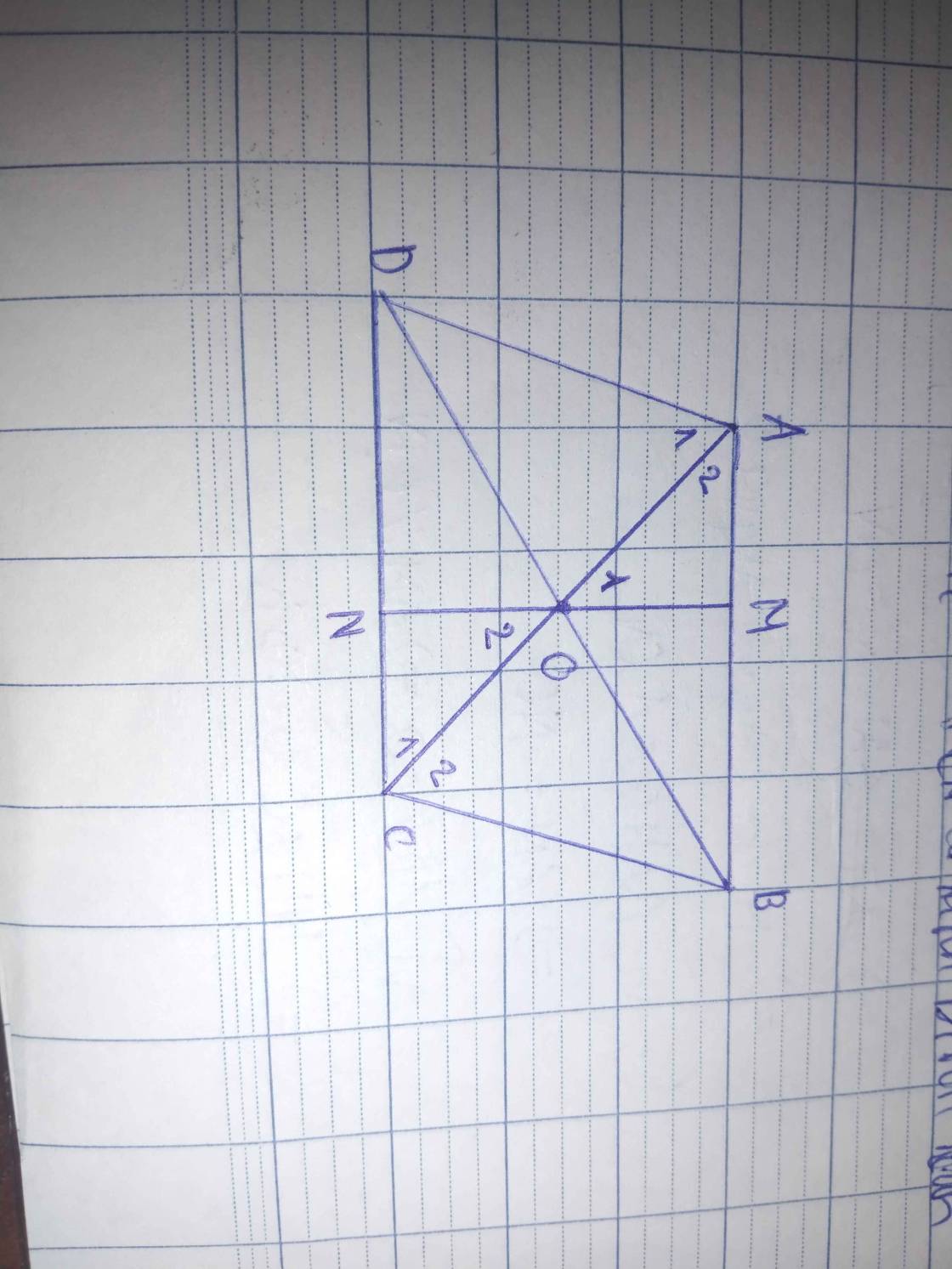
a: Xét ΔMAO và ΔNCO có
\(\widehat{MAO}=\widehat{NCO}\)
OA=OC
\(\widehat{AOM}=\widehat{CON}\)
Do đó: ΔMAO=ΔNCO
Suy ra: MO=NO
hay M đối xứng với N qua O

Câu 20:
a: \(2x^3-8x^2+8x=2x\left(x-2\right)^2\)
b: \(2xy+2x+yz+z=\left(y+1\right)\left(2x+z\right)\)
c: \(x^2+2x+1-y^2=\left(x+1-y\right)\left(x+1+y\right)\)

Cau 20:
a: \(2x^3-8x^2+8x=2x\left(x-2\right)^2\)
b: \(2xy+2x+yz+z=\left(y+1\right)\left(2x+z\right)\)
c: \(x^2+2x+1-y^2=\left(x+1-y\right)\left(x+1+y\right)\)

Câu 20:
a: \(2x^3-8x^2+8x\)
\(=2x\left(x^2-4x+4\right)\)
\(=2x\left(x-2\right)^2\)
b: \(2xy+2x+yz+z\)
\(=2x\left(y+1\right)+z\left(y+1\right)\)
\(=\left(y+1\right)\left(2x+z\right)\)

\(19,\\ a,=4x^3-4x^2-4x-2x^2+x+1=4x^3-6x^2-3x+1\\ b,=2x^2+4x-1\\ c,=\left(6x^3+9x^2-16x^2-24x+8x+12\right):\left(2x+3\right)\\ =\left(2x+3\right)\left(3x^2-8x+4\right):\left(2x+3\right)=3x^2-8x+4\)
\(20,\\ a,=2x\left(x^2-4x+4\right)=2x\left(x-2\right)^2\\ b,=2x\left(y+1\right)+z\left(y+1\right)=\left(y+1\right)\left(2x+z\right)\\ c,=\left(x+1\right)^2-y^2=\left(x-y+1\right)\left(x+y+1\right)\)
\(21,\)
Để \(A\left(x\right)⋮B\left(x\right)\Leftrightarrow3x^2+5x+m=\left(x-2\right)\cdot C\left(x\right)\)
Thay \(x=2\Leftrightarrow12+10+m=0\Leftrightarrow m=-22\)

a)
Do ABCD là hình thoi :
=> AB // CD=) AM // CN
Do AM // CN
=> \(\widehat{MAO}=\widehat{NCO}\) ( 2 góc so le trong )
Do ABCD là hình thoi:
Mà O là giao điểm của 2 đường chéo
=> AO = CO ( vì hình thoi có tất cả các tính chất hình bình hành ) => O là trung điểm của AC
Xét tam giác AOM và tam giác CON có :
\(\widehat{AOM}=\widehat{CON}\)( đối đỉnh )
AO = CO
\(\widehat{MAO}=\widehat{NCO}\)(chứng minh trên)
=> Δ AOM = Δ CON ( g-c-g )
b) Do Δ AOM = Δ CON ( chứng minh phần a)
=) OM = ON (2 cạch tương ứng)
=> O là trung điểm của MN
Xét tứ giác AMCN có :
2 đường chéo AC và MN cắt nhau tại trung điểm O
=> AMCN là hình bình hành

Do ABCD là hình thoi :
=) AB // CD=) AM // CN
Do AM // CN
=) \(\widehat{MAO}\)=\(\widehat{NCO}\) ( 2 góc so le trong )
Do ABCD là hình thoi:
Mà O là giao điểm của 2 đường chéo
=) AO=CO ( vì hình thoi có tất cả các tính chất hình bình hành ) =) O là trung điểm của AC
Xét tam giác AOM và tam giác CON có :
\(\widehat{AOM}\)=\(\widehat{CON}\)( đối đỉnh )
AO=CO
\(\widehat{MAO}\)=\(\widehat{NCO}\)(chứng minh trên)
=) Tam giác AOM = Tam giác CON ( g-c-g )
b) Do tam giác AOM = Tam giác CON ( chứng minh phần a)
=) OM=ON (2 cạch tương ứng)
=) O là trung điểm của MN
Xét tứ giác AMCN có :
2 đường chéo AC và MN cắt nhau tại trung điểm O
=) AMCN là hình bình hành
a) Trong hình thoi ABCD có:
\(\widehat{BAD}=\widehat{BCD}\)(2 góc đối của hình thoi)
\(\Rightarrow\widehat{BAO}+\widehat{OAD}=\widehat{BCO}+\widehat{OCD}\)
\(\Rightarrow\widehat{BAO}=\widehat{OAD}=\widehat{BCO}=\widehat{OCD}\)(2 đường chéo là tia phân giác của các góc)
\(\Rightarrow\widehat{MAO}=\widehat{OAD}=\widehat{BCO}=\widehat{OCD}\)
Xét \(\Delta AOM\)và \(\Delta CON\)có:
\(\widehat{MOA}=\widehat{NOC}\)(2 góc đối đỉnh)
\(OA=OC\)(2 đường chéo cắt nhau tại trung điểm mỗi đường)
\(\widehat{MAO}=\widehat{NCO}\)(Chứng minh trên)
Do đó \(\Delta AOM=\Delta CON\left(g.c.g\right)\)
b) Vì \(\Delta AOM=\Delta CON\)(câu a)
\(\Rightarrow OM=ON\)(2 cạnh tương ứng)
Tứ giác AMCN có:
OA = OC (gt)
OM = ON (chứng minh trên)
\(\Rightarrow\)Tứ giác AMCN là hình bình hành
a) hình bình hành ABCD có:
O là giao điểm của AC và BD
=> O là trung điểm của AC và BD
xét tam giác AOM và tam giác NOC có:
AO= CO
góc A² = góc C¹ (so le trong)
góc O¹=góc O² (đối đỉnh)
=> tam giác AOM=tam giác CON(g.c.g) => OM =ON
=> M đối xứng với N qua O
b) tam giác AOM= tam giác CON nên
=> AM= CN, AM // CN
=> tứ giác AMNC là hình bình hành