Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

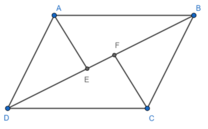
Ta có S A B C F E = S A B E + S B F C S A D C F E = S D F C + S D A E
Xét hình bình hàng ABCD có AE và CF lần lượt là phân giác của các góc A và C
nên suy ra: B A E ^ = D A E ^ = B C F ^ = D C F ^
Xét ΔABE và ΔDCF có:
AB = CD (gt), A B E ^ = C D F ^ (slt), B A E ^ = D C F ^ (cmt)
=> ΔABE = ΔDCF (g.c.g)
=> SABE = SCDF (1)
Xét ΔBCF và ΔDAE có:
AD = BC (gt), A D E ^ = C B F ^ (slt), D A E ^ = B C F ^ (cmt)
=> ΔBCF = ΔDAE (g.c.g)
=> SBCF = SDAE (2)
Từ (1) và (2) suy ra:
SABE + SBCF = SCDF + SDAE
=> SABCFE = SADCFE
Đáp án cần chọn là: C

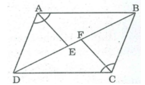
Ta có:
△ ABE = △ CDF (g.c.g) ⇒ S A B E = S C D F (l)
△ AED = △ CFB (g.c.g) ⇒ S A E D = S C F B (2)
Từ (1) và (2) ⇒ S A B E + S C F B = S C D F + S A E D
Hay S A B C F E = S A D C F E

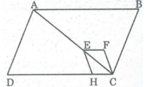
Hình ABCFE không phải là tứ giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh CF.

a: Xét tứ giác DEBF có
BE//DF
BE=DF
Do đó: DEBF là hình bình hành
b: Vì DEBFlà hình bình hành
nên DB cắt EF tại trung điểm của mỗi đường(1)
Vì ABCD là hình bình hành
nên AC cắt BD tại trung điểm của mỗi đường(2)
Từ (1), (2) suy ra E,O,F thẳng hàng
c: Để DEBF là hình thoi thì DE=BE=AB/2
Xét ΔDAB có
DE là trung tuyến
DE=AB/2
Do đo:ΔDAB vuông tại D
=>DA vuông góc với DB

a: Xét ΔAED vuông tại E và ΔCFB vuông tại F có
AD=CB
\(\widehat{ADE}=\widehat{CBF}\)
Do đó: ΔAED=ΔCFB
Suy ra AE=CF: ED=FB
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
b: Xét ΔKBF vuông tại F và ΔIDE vuông tại E có
FB=ED
\(\widehat{KBF}=\widehat{IDE}\)
Do đó: ΔKBF=ΔIDE
Suy ra: KB=ID
Xét tứ giác KBID có
KB//ID
KB=ID
Do đó: KBID là hình bình hành
Suy ra: Hai đường chéo KI và BD cắt nhau tại trung điểm của mỗi đường


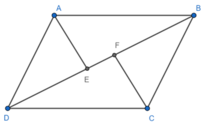
Hình ABCFE không phải là đa giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh EF.
Hình ADCFE không phải là đa giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh EF.