NQ
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 12 2021
\(AB^2+CD^2-\left(BC^2+DA^2\right)=\overrightarrow{AB}^2+\overrightarrow{CD}^2-\overrightarrow{BC}^2-\overrightarrow{AD}^2\)
\(=\left(\overrightarrow{AB}+\overrightarrow{AD}\right)\left(\overrightarrow{AB}-\overrightarrow{AD}\right)+\left(\overrightarrow{CD}-\overrightarrow{BC}\right)\left(\overrightarrow{CD}+\overrightarrow{BC}\right)\)
\(=\overrightarrow{DB}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)+\overrightarrow{DB}\left(\overrightarrow{BC}+\overrightarrow{DC}\right)\)
\(=\overrightarrow{DB}\left(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{BC}+\overrightarrow{DC}\right)\)
\(=2\overrightarrow{AC}.\overrightarrow{DB}\) (đpcm)
CM
24 tháng 5 2019
Chọn C
Theo đầu bài ta có: AC2 + BD2 = AD2 + BC2 nên AC2 - AD2 = BC2 - BD2
Suy ra:
Hay
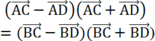
Tương đương
HP
17 tháng 12 2020
a, \(\left(\overrightarrow{AC}-\overrightarrow{AB}\right)^2=\overrightarrow{BC}^2\)
\(\Leftrightarrow AC^2+AB^2-2\overrightarrow{AB}.\overrightarrow{AC}=BC^2\)
\(\Leftrightarrow2\overrightarrow{AB}.\overrightarrow{AC}=AB^2+AC^2-BC^2\)
\(\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=\dfrac{AB^2+AC^2-BC^2}{2}=\dfrac{5^2+8^2-7^2}{2}=20\)
b, \(2\overrightarrow{CA}.\overrightarrow{CB}=CA^2+CB^2-BC^2=CA^2\)
\(\Rightarrow\overrightarrow{CA}.\overrightarrow{CB}=\dfrac{CA^2}{2}=\dfrac{8^2}{2}=32\)
AH
Akai Haruma
Giáo viên
17 tháng 12 2020
Lời giải:
a)
\(\overrightarrow{AC}-\overrightarrow{AB}=\overrightarrow{BC}\)
\(\Rightarrow (\overrightarrow{AC}-\overrightarrow{AB})^2=\overrightarrow{BC}^2\Leftrightarrow AB^2+AC^2-2\overrightarrow{AC}.\overrightarrow{AB}=BC^2\)
\(\Leftrightarrow 2\overrightarrow{AB}.\overrightarrow{AC}=AB^2+AC^2-BC^2\) (đpcm)
Ta có:
\(\overrightarrow{AB}.\overrightarrow{AC}=\frac{AB^2+AC^2-BC^2}{2}=\frac{5^2+8^2-7^2}{2}=20\)
\(\cos \angle A=\frac{\overrightarrow{AB}.\overrightarrow{AC}}{|\overrightarrow{AB}|.|\overrightarrow{AC}|}=\frac{20}{5.8}=\frac{1}{2}\)
\(\Rightarrow \angle A=60^0\)
b)
Tương tự phần a, \(\overrightarrow{CA}.\overrightarrow{CB}=\frac{CA^2+CB^2-AB^2}{2}=\frac{8^2+7^2-5^2}{2}=44\)
CM
15 tháng 2 2019
Đáp án: D
a sai vì nếu tam giác ABC thỏa mãn AB2 + AC2 = BC2 thì tam giác ABC vuông tại A không phải vuông tại B.
b, c, d đúng.
M
1
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2020
Ta có:
\(BC\left(AC.cosC-AB.cosB\right)=BC.AC.cosC-AB.BC.cosB\)
\(=BC.AC.\dfrac{BC^2+AC^2-AB^2}{2BC.AC}-AB.BC.\dfrac{AB^2+BC^2-AC^2}{2AB.BC}\)
\(=\dfrac{BC^2+AC^2-AB^2}{2}-\dfrac{AB^2+BC^2-AC^2}{2}\)
\(=AC^2-AB^2\) (đpcm)
HH
0
Ta có: \(AC^2+BD^2=\left(\overrightarrow{AB}+\overrightarrow{AD}\right)^2+\left(\overrightarrow{BC}+\overrightarrow{BA}\right)^2\)
\(=AB^2+AD^2+2\overrightarrow{AB}.\overrightarrow{AD}+BC^2+BA^2+2\overrightarrow{BA}.\overrightarrow{BC}\)
\(=AB^2+AD^2+BC^2+AD^2+2\overrightarrow{AB}\left(\overrightarrow{AD}-\overrightarrow{BC}\right)\)
\(=AB^2+AD^2+BC^2+AD^2\)