Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha
a) Do ABCD là hình bình hành ⇒ Góc A = góc C
⇒ \(\dfrac{1}{2}\)góc A = \(\dfrac{1}{2}\)góc C ⇒ Góc DAM = Góc BCN
Xét tam giác ADM và tam giác CBN có:
AD = BC ( ABCD là hình bình hành)
Góc DAM = góc CBN ( Chứng minh trên )
Góc ADB = góc ABC ( ABCD là hình bình hành )
⇒ Tam giác ADM = tam giác CBN (g.c.g)
⇒ BN = DM ( 2 cạnh tương ứng )
Vì ABCD là hình bình hành ⇒ AB = CD
⇒ BN + AN = CM + DM.
Mà BN = DM ⇒ AN = MC. Do AN song song với MC ( vì AB song song với CD)
ANCM là hình bình hành.
b) Xét tứ giác BMDN có BN = DM ; BN song song với DM ( do AB song song với CD)
⇒ BMDN là hình bình hành ⇒ BM = DN

ABCD là hình bình hành
=> AD = BC (tc)
góc ADC = góc CBA (tc) (1)
góc DAB = góc BCD (tc) (2)
AM; CN là phân giác của góc DAB; góc BCD (Gt)
=> DAM = 1/2. góc DAB và BCN = 1/2. góc BCD (tc)
=> góc DAM = góc BCN ; (1)(2)
=> tam giác ADM = tam giác CBN (g-c-g)
=> AM = NC (đn)
có AN // MC do ABCD là hình bình hành (gt)
=> ANCM là hình bình hành (dh)

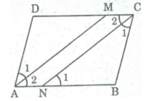
Ta có: ∠ A = ∠ C (tính chất hình bình hành)
∠ A 2 = 1/2 ∠ A ( Vì AM là tia phân giác của ∠ (BAD) )
∠ C 2 = 1/2 ∠ C ( Vì CN là tia phân giác của ∠ (BCD) )
Suy ra: ∠ A 2 = ∠ C 2
Do ABCD là hình bình hành nên AB // CD (gt)
Hay AN // CM (1)
Mà ∠ N 1 = ∠ C 2 (so le trong)
Suy ra: ∠ A 2 = ∠ N 1
⇒ AM // CN (vì có cặp góc ở vị trí đồng vị bằng nhau) (2)
Từ (1) và (2) suy ra tứ giác AMCN là hình bình hành.

a) Do AM = DN Þ MADN là hình bình hành
⇒ D ^ = A M N ^ = E M B ^ = M B C ^
Ta có DMPE = DBPE nên EP = FP. Vậy MEBF là hình thoi và 2 điểm E, F đối xứng nhau qua AB.
b) Tứ giác MEBF có MB Ç EF = P; Lại có P trung điểm BM, P là trung điểm EF, MB ^ EF.
Þ MEBF là hình thoi.
c) Để BNCE là hình thang cân thì C N E ^ = B E N ^
Mà
C N E ^ = D ^ = M B C ^ = E B M ^ nên DMEB có 3 góc bằng nhau, suy ra điều kiện để BNCE là hình thang cân thì A B C ^ = 60 0