Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng Talet vào tam giác AEM có AE//CD
\(\frac{AM}{CM}=\frac{1}{3}\Rightarrow\frac{AM}{AC}=\frac{1}{4}\Rightarrow S_{ADM}=\frac{1}{4}S_{ADC}=\frac{1}{8}S\)
Tương tự: \(\frac{CN}{AN}=\frac{1}{2}\Rightarrow\frac{CN}{AC}=\frac{1}{3}\Leftrightarrow S_{DNC}=\frac{1}{3}S_{ADC}=\frac{1}{6}S\)
Có: \(S_{DMN}=S_{ADC}-S_{ADM}-S_{DNC}=\frac{1}{2}S-\frac{1}{8}S-\frac{1}{6}S=\frac{5}{24}S\)

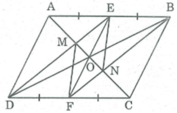
Xét ∆ EOM và ∆ FON có: ∠ (MEO) = ∠ (NFO) (so le trong do DE//BF)
OE = OF (tính chất hình bình hành)
∠ (MOE)= ∠ (NOF) (đối đỉnh )
Suy ra: ∆ EOM = ∆ FON (g.c.g) ⇒ OM = ON
Vậy tứ giác EMFN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường).
#)Trả lời :
giải ra giùm mink cái